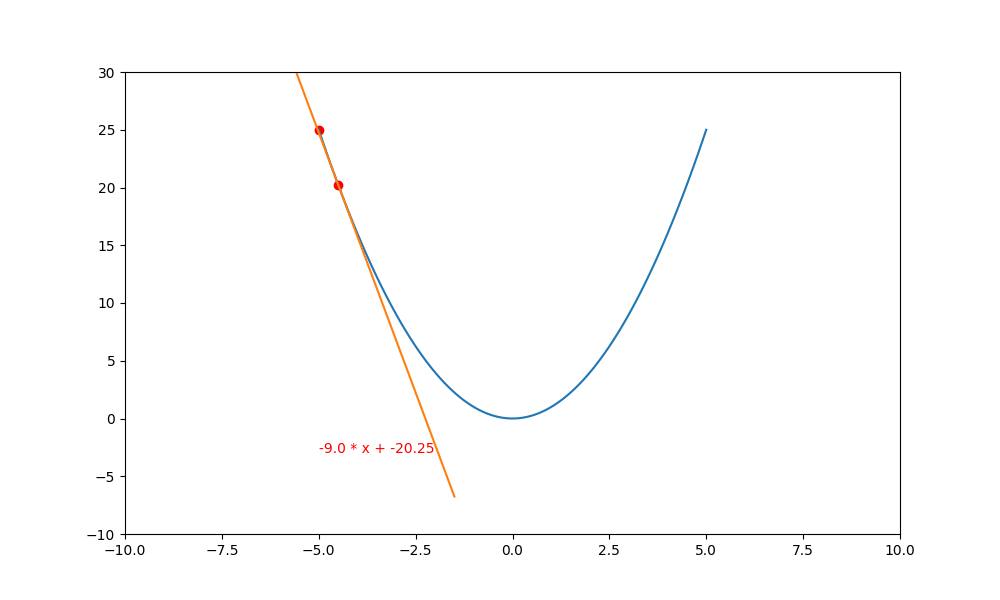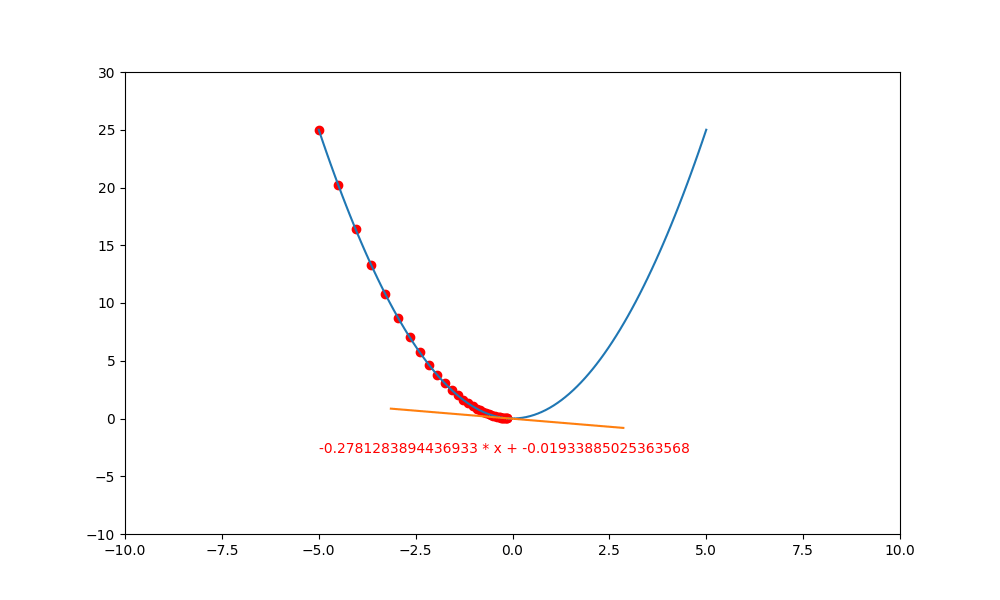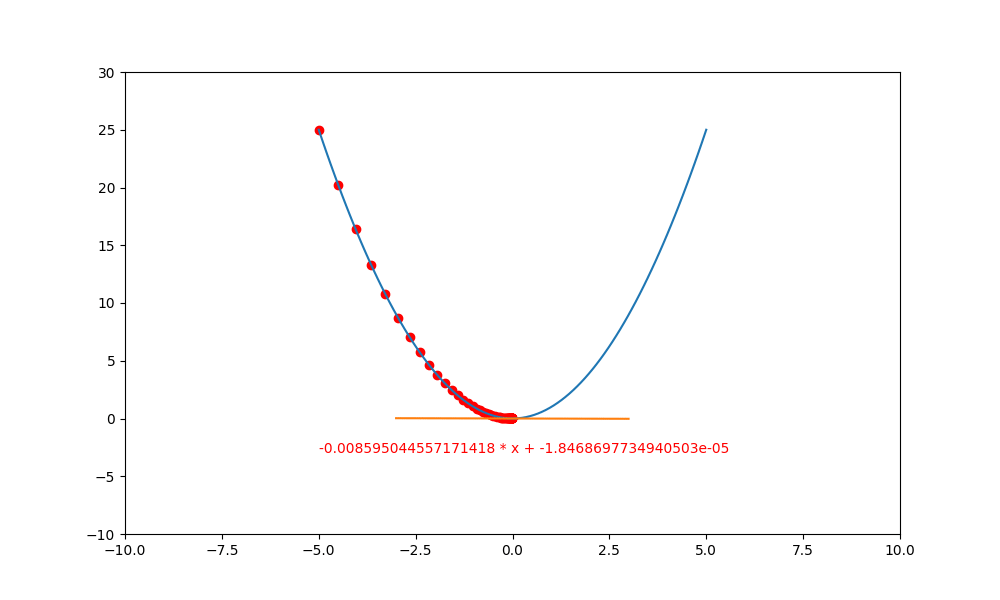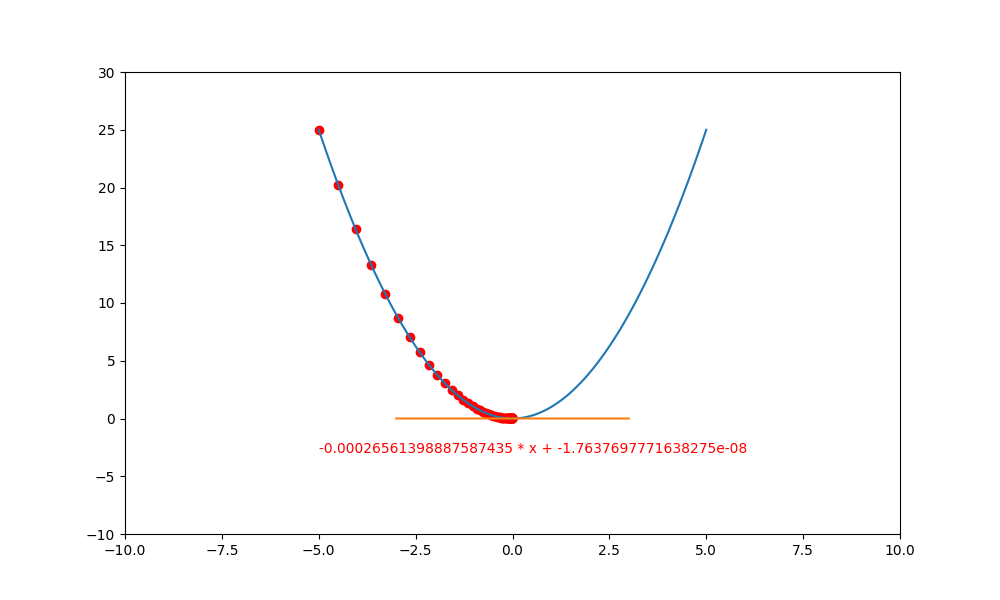
底下使用 PyTorch 計算 $(y=x^2)$ 的梯度下降。
import torch as tc
import pylab as plt
import numpy as np
def f(x):
if tc.is_tensor(x):
return x.square()
else:
return np.square(x)
x = np.linspace(-5, 5, 100)
y=f(x)
fig=plt.figure(figsize=(9,6))
ax=fig.subplots()
epochs=100
lr=0.2
tx=tc.tensor([-5.], requires_grad=True)
history=[]
for i in range(epochs):
f(tx).backward()
with tc.no_grad():
now_x = tx.numpy()[0]
history.append(now_x)
a = tx.grad.numpy()[0]
b=f(now_x) - a * now_x
ax.clear()
plt.plot(x, y, c='b')
plt.scatter(history, f(history), c='r')
ax.set_xlim(-10, 10)
ax.set_ylim(-2, 35)
xl = now_x - 2
xr = now_x + 2
plt.plot([xl, xr], [a * xl + b, a * xr + b], c='orange')
tx -= tx.grad * lr
tx.grad.zero_()
plt.pause(0.01)
plt.show()
一元四次迴歸線逼近法
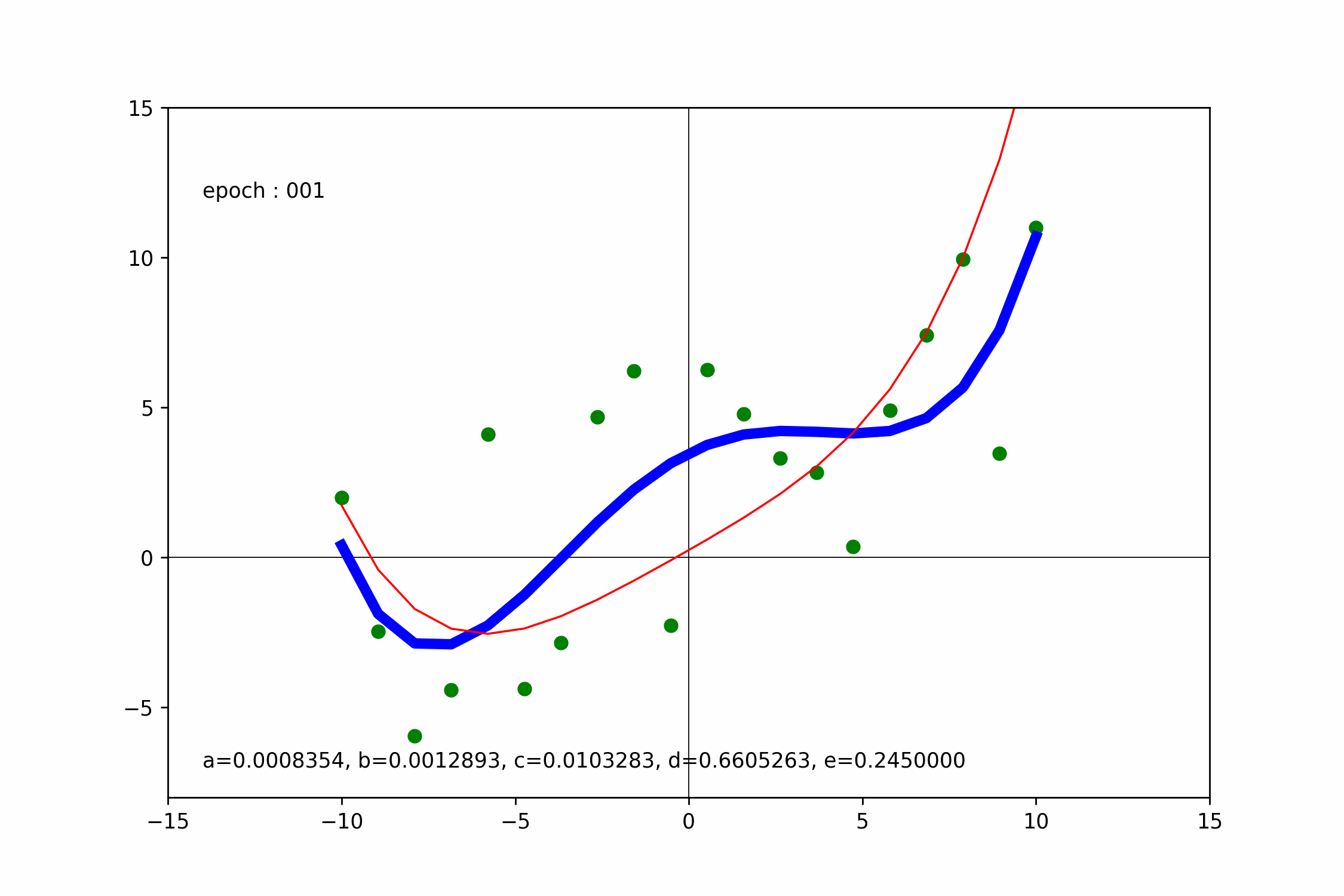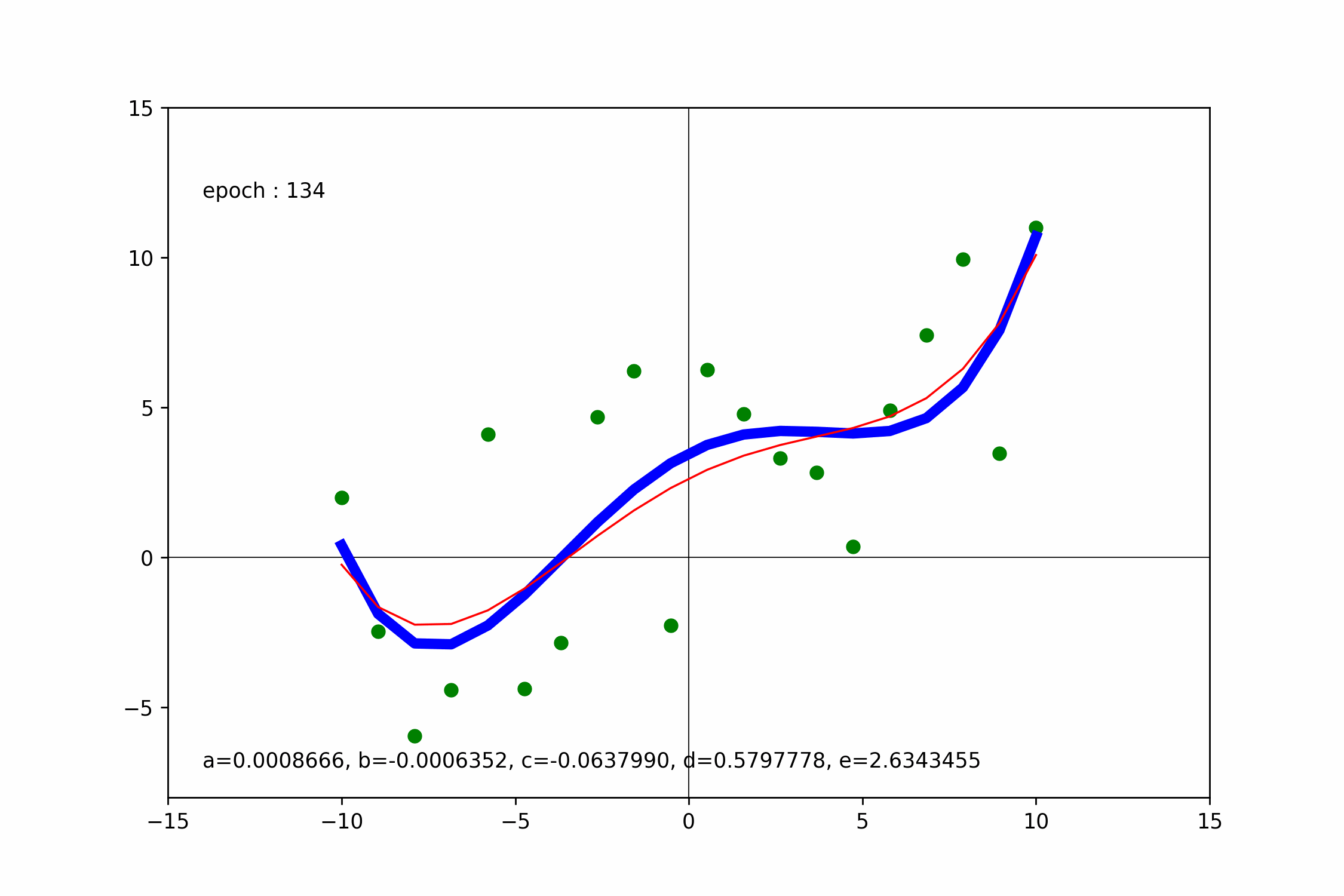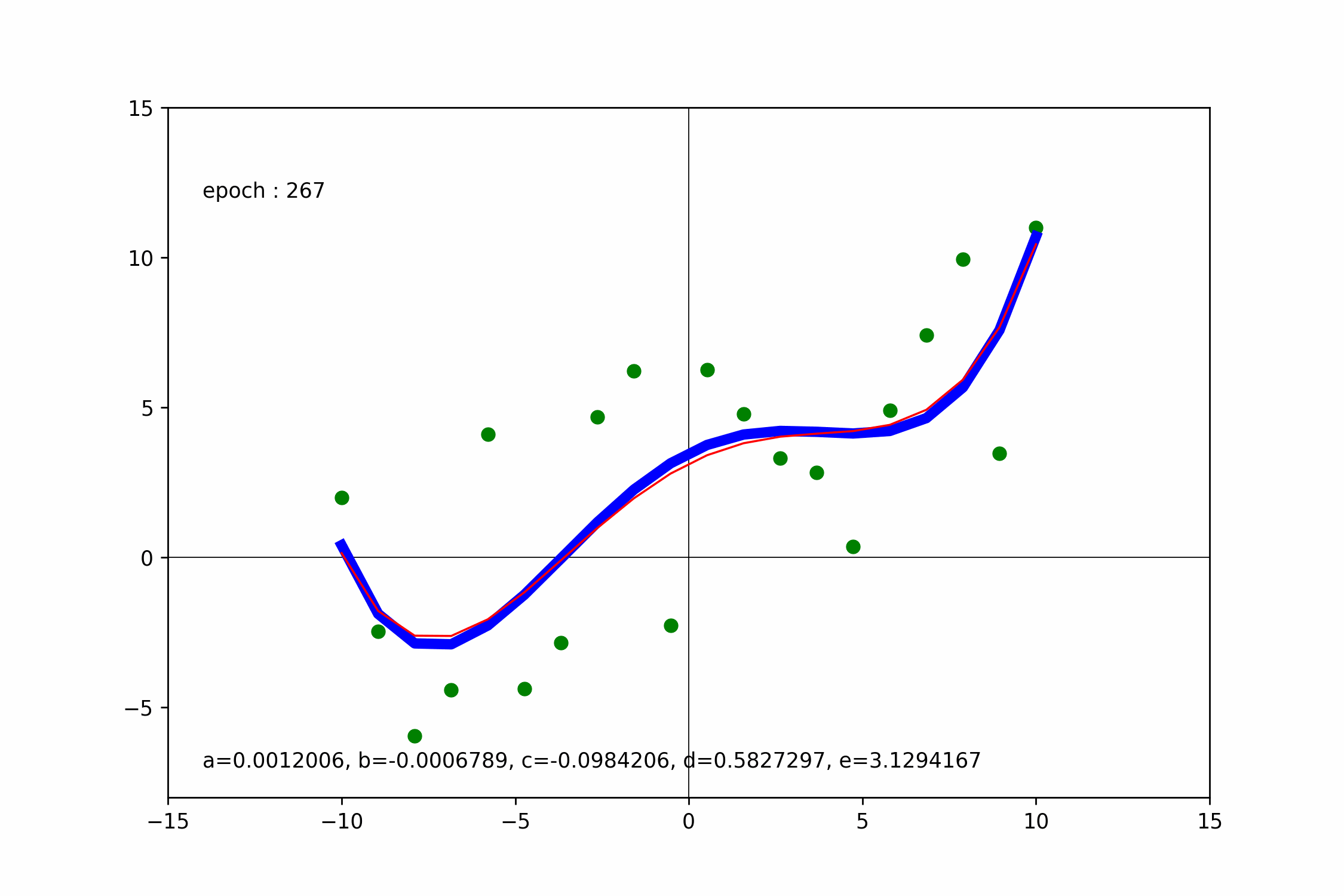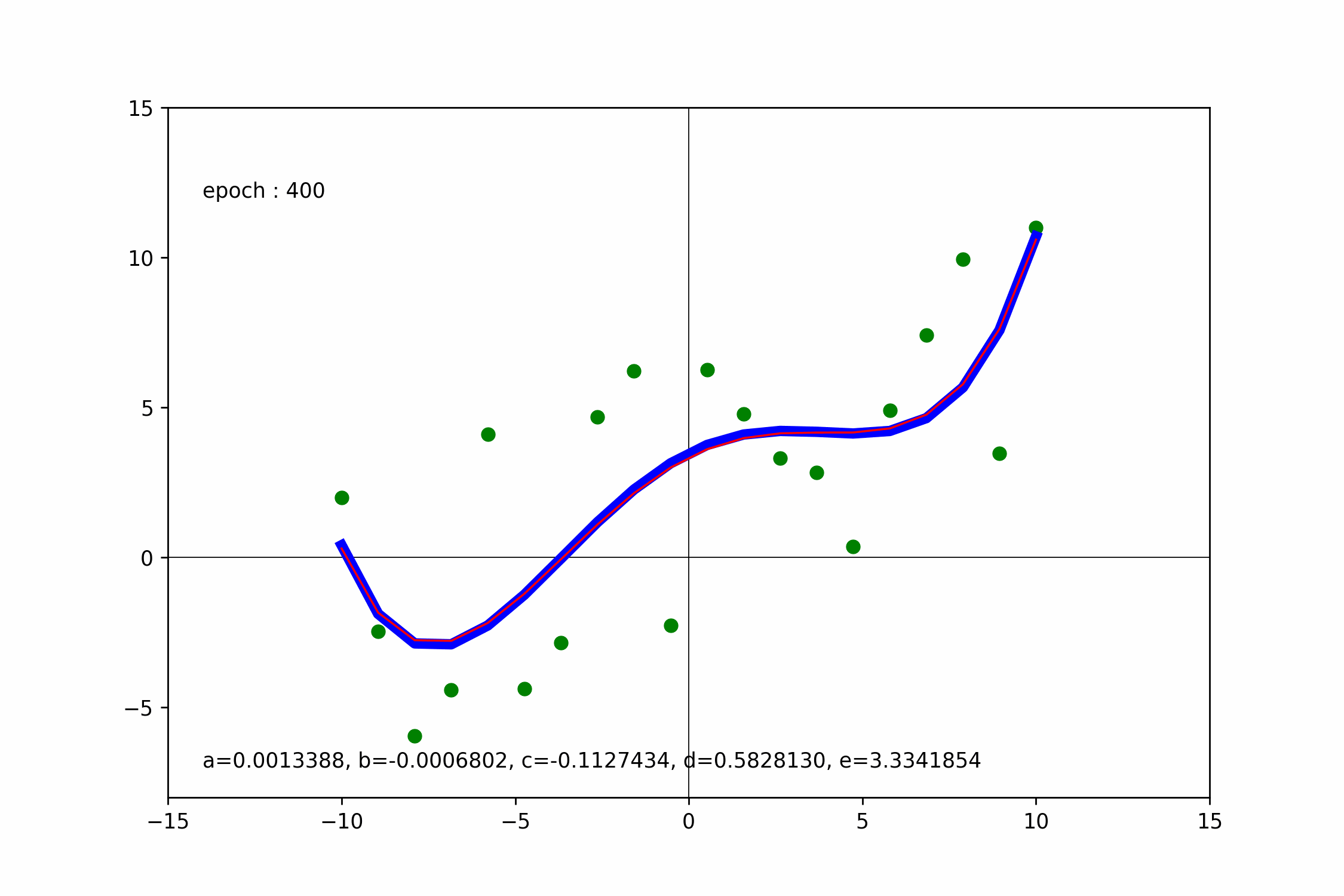
底下使用 PyTorch 梯度下降求一元四次迴歸線。
import numpy as np
import torch as tc
import pylab as plt
def f(a, b, c, d, e):
return tc.sum(
tc.square(
ty-(
a * tx.pow(4) +
b * tx.pow(3) +
c * tx.pow(2) +
d * tx +
e
)
)
)
n=20
np.random.seed(10)
x = np.linspace(-10,10 ,n)
y = 0.5*x+3 + np.random.randint(-5,5, n)
tx = tc.tensor(x)
ty = tc.tensor(y)
fig = plt.figure(figsize=(9,6))
ax = fig.subplots()
epochs=400
lr=2.5e-3
a=tc.tensor([0.], requires_grad=True)
b=tc.tensor([0.], requires_grad=True)
c=tc.tensor([0.], requires_grad=True)
d=tc.tensor([0.], requires_grad=True)
e=tc.tensor([0.], requires_grad=True)
for i in range(epochs):
ax.clear()
ax.set_xlim(-15, 15)
ax.set_ylim(-8, 15)
ax.plot([-15,15], [0,0], c='k', linewidth=0.5)
ax.plot([0,0], [-8,15], c='k', linewidth=0.5)
ax.scatter(x, y, c='g')
reg = np.poly1d(np.polyfit(x, y, 4))
ax.plot(x, reg(x), c="b", linewidth=5)
f(a,b,c,d,e).backward()
with tc.no_grad():
a -= a.grad * lr * 1e-6
b -= b.grad * lr * 1e-5
c -= c.grad * lr * 1e-3
d -= d.grad * lr * 1e-1
e -= e.grad * lr
ax.plot(x,
a.numpy()[0] * np.power(x, 4)+
b.numpy()[0] * np.power(x, 3) +
c.numpy()[0] * np.power(x ,2) +
d.numpy()[0] * x +
e.numpy()[0],
c='r', linewidth=1)
a.grad.zero_();b.grad.zero_();c.grad.zero_();d.grad.zero_();e.grad.zero_();
ax.text(-14, 12, f'epoch : {i+1:03d}')
ax.text(
-14,-7,
f'a={a.numpy()[0]:.7f}, b={b.numpy()[0]:.7f}, c={c.numpy()[0]:.7f}, d={d.numpy()[0]:.7f}, e={e.numpy()[0]:.7f}'
)
plt.pause(0.01)
plt.show()
一元 n 次迴歸線逼近法
底下代碼是經由上述代碼進行優化,可以計算一元 n 次迴歸線逼近。只要更改 order (次方) 及 scale 的值即可,scale 的 size 必需是 order + 1 。
import numpy as np
import torch as tc
import pylab as plt
#from celluloid import Camera
def f(params):
str_f='tc.mean(tc.square(tc.tensor(y)-('
for i in range(order+1):
str_f += f'params[{i}] * tx.pow({order-i}) +'
str_f = str_f[:-1]+ ")))"
return eval(str_f)
order=5
scale=[1e-7, 1.8e-5, 1.2e-3, 5.0e-2, 2.0e-0, 1.2e2]
n=100
np.random.seed(10)
x=np.linspace(-10,10 ,n)
y=0.5*x+3 + np.random.randint(-5,5, n)
tx = tc.tensor(x)
ty = tc.tensor(y)
fig=plt.figure(figsize=(9,6))
ax=fig.subplots()
#camera = Camera(fig)
epochs=1500
lr=2.6e-3
params=[tc.tensor([0.], requires_grad=True) for i in range(order+1)]
for epoch in range(epochs):
ax.clear()
ax.set_xlim(-15, 15)
ax.set_ylim(-8, 15)
ax.plot([-15,15], [0,0], c='k', linewidth=0.5)
ax.plot([0,0], [-8,15], c='k', linewidth=0.5)
ax.scatter(x, y, c='g', s=5)
reg = np.poly1d(np.polyfit(x, y, order))
ax.plot(x, reg(x), c="b", linewidth=5)
f(params).backward()
with tc.no_grad():
for i in range(order+1):
params[i] -= params[i].grad * lr * scale[i]
str_f=""
for i in range(order+1):
str_f += f'params[{i}].numpy()[0] * np.power(x, {order-i})+'
str_f = str_f[:-1]
ax.plot(x,eval(str_f),c='r', linewidth=1)
ax.text(-14, 12, f'epoch : {epoch+1:03d}')
txt=''
for i in range(order+1):
txt += f'p[{i}]:{params[i].numpy()[0]:10.7f}\n'
params[i].grad.zero_()
ax.text(-14,-8,txt)
for i in range(order+1):
params[i].grad.zero_()
#camera.snap()
plt.pause(0.01)
# animation = camera.animate()
# animation.save('pytorch_reg.gif', fps=30)
plt.show()

