為什麼叫 Q-Learning
Q 這個字母在強化學習中表示一個動作的期望獎勵。那為什麼叫 Q learning,而不是 R learning、V learning 呢! 應該是一個叫 “阿Q哥” 的人發明的演算法,隨便給個名字而以。反正網路上也查不到發明者,而世上那麼多演算法,有如過街老鼠般的多,就隨便給個名字。
公式
先背一下Q-Learning 的公式
$(Q(s,a)=Q(s,a)+lr[r+\gamma*maxQ(s’)-Q(s,a)])$
請注意,上面的公式並不是數學公式,而是程式的語法。”=” 左邊是下一次迴圈 Q(s,a) 的值,”=” 右邊是上一次迴圈所計算出來的 Q(s,a) 值。
轉換成Python 的語言如下
if s_next != 'terminal':
target = reward + gamma * table.iloc[s_next, :].max()
else:
target = 1 #也可以使用 target = reward(因為終點為 1)
runFlag = False#終止此 epoch
table.loc[s, a] = table.loc[s,a] + lr * (target - table.loc[s,a])
六道迴輪
要用例子來說明 Q-Learning 其實有困難,因為都不太容易懂,在此用佛教的輪迴來說明。首先請大家先記一下,佛教闡述這大千世界有 “慾界”,”色界”,”無色界” 這三界。我們目前處於慾界,至於色界及無色界是什麼現像,請看官們自行上網查詢。
慾界有六道輪迴,分別為 “地獄(s0)”、”餓鬼(s1)”、”畜牲(s2)”、”人道(s3)”、”阿修羅(s4)”、”天道(s5)”。天道就是玄天上帝等神明的境界。神明也是要進行修行的啦,才能進入色界及無色界。
我們先簡化六道輪迴,轉世為 “天道” 是最終目的,位於最右邊,能獲得回報值 “1” (修成正果)。其它的轉世,不論是人變畜牲,或畜牲變人回報值都是 “0”。雖說這不符合天理,但這只是為了簡化問題而以,請大家耐心接受。
假設有六個生靈,分別處於這六道之中,然後這六個生靈可以選擇 “修行(往右)” 或 “不修行(往左)”。
第 0 世(epoch 0)
一開始,天道(s5) 往左往右都不行,因為往右沒路了,所以為 0 。往左也沒回報,所以也是 0。
但修羅(s4) 卻不一樣,往右(修行) 可以得到回報 1,然後經過上面公式東扣西減(Q公式),得到 0.1的值。但如果往左(不修行),得到 0 的值。
那麼s0~s3呢! 反正就是爛命一條,有修沒修都是 0。
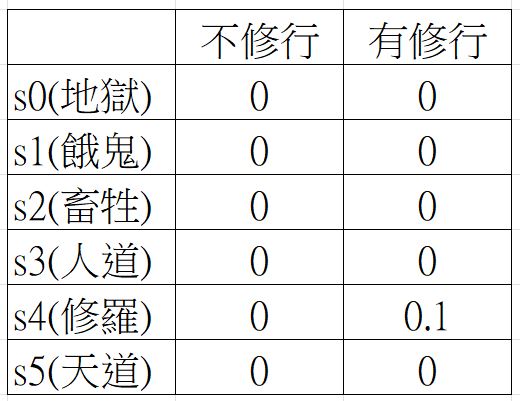
第 1 世(epoch 1)
第 1 世時,依公式計算
Q(s3, right)=
= Q(s3, right) + $(lr[r+\gamma*maxQ(s4,a)-Q(s3,right)])$
=0 + 0.1 * (0 + 0.9 * 0.1 – 0)
=0.09
Q(s4,right)
= Q(s4, right) + $(lr[r+\gamma*maxQ(s5,a)-Q(s4,right)])$
= 0.1 + 0.1 * (1+ 0.9 * 0 – 0.1)
= 0.1 + 0.1 * 0.9
= 1.9
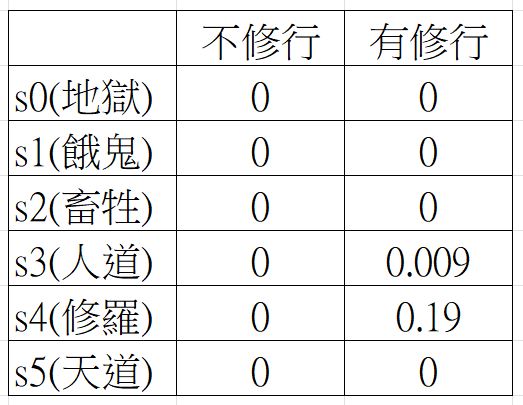
經過幾世的探測後,因為使用 $(\gamma*maxQ(s’,a’))$,本次狀態會依下次狀態的最大值走,所以 steps 就會愈來愈少,愈快達到 s5(天道) 的狀態。
完整代碼
完整代碼如下
import numpy as np
import pandas as pd
import time
np.random.seed(1)
status = 6#一維長度
actions = ['left', 'right']# available actions
epsilon = 0.9 # greedy police
lr = 0.1 # learning rate
gamma = 0.9 # discount factor
epochs = 20 # maximum episodes
delay = 0.1 # fresh time for one move
def build_table(status, actions):
table = pd.DataFrame(
np.zeros((status, len(actions))),
columns=actions,
)
#print(table.round({"left":10, "right":10}))
print(table)
return table
def choose_action(status, table):
#選擇要執行的動作
state_actions = table.iloc[status, :]
if (np.random.uniform() > epsilon) or ((state_actions == 0).all()):#亂數選擇動作
action_name = np.random.choice(actions)
else:#貪婪模式
action_name = state_actions.idxmax()# replace argmax to idxmax as argmax means a different function in newer version of pandas
return action_name
def get_reward(s, action):
# 取得獎勵值
if action == 'right': #往右移
if s == status - 2: #終點
s_next = 'terminal'
reward = 1
else:
s_next = s + 1
reward = 0
else: #往左移
reward = 0
if s == 0:
s_next = s #已達最左邊
else:
s_next = s - 1
return s_next, reward
def show(s, episode, step_counter):
#顯示結果
env_list = ['-']*(status-1) + ['T'] # '---------T' our environment
if s == 'terminal':
print(f'\nEpisode {episode+1}: total steps = {step_counter}')
time.sleep(0.5)
print('\r', end='')
else:
env_list[s] = 'o'
interaction = ''.join(env_list)
print(f'\r{interaction}', end='')
time.sleep(delay)
def rl():
#強化學習主程式
table = build_table(status, actions)
for e in range(epochs):
step_counter = 0
s = 0
runFlag = True
show(s, e, step_counter)
while runFlag:
a = choose_action(s, table)
s_next, reward = get_reward(s, a) # take action & get next state and reward
if s_next != 'terminal':
target = reward + gamma * table.iloc[s_next, :].max()
else:
target = 1 #也可以使用 target = reward(因為終點為 1)
runFlag = False#終止此 epoch
table.loc[s, a] = table.loc[s,a]+lr * (target - table.loc[s,a]) # update
s = s_next#移到下一個狀態
show(s, e, step_counter+1)
step_counter += 1
print("\r")
print(table.applymap(lambda x: '%.10f' % x))
return table
if __name__ == "__main__":
table = rl()
print('最後的 table:')
print(table.applymap(lambda x: '%.10f' % x))
結果如下
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0
----oT
Episode 1: total_steps = 6
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.1
5 0.0 0.0
----oT
Episode 2: total_steps = 11
left right
0 0.0 0.000
1 0.0 0.000
2 0.0 0.000
3 0.0 0.009
4 0.0 0.190
5 0.0 0.000
----oT
Episode 3: total_steps = 6
left right
0 0.0 0.00000
1 0.0 0.00000
2 0.0 0.00081
3 0.0 0.02520
4 0.0 0.27100
5 0.0 0.00000
----oT
Episode 4: total_steps = 10
left right
0 0.0 0.000000
1 0.0 0.000073
2 0.0 0.002997
3 0.0 0.047070
4 0.0 0.343900
5 0.0 0.000000
----oT
Episode 5: total_steps = 5
left right
0 0.0 0.000007
1 0.0 0.000335
2 0.0 0.006934
3 0.0 0.073314
4 0.0 0.409510
5 0.0 0.000000
----oT
Episode 6: total_steps = 5
left right
0 0.0 0.000036
1 0.0 0.000926
2 0.0 0.012839
3 0.0 0.102839
4 0.0 0.468559
5 0.0 0.000000
----oT
Episode 7: total_steps = 5
left right
0 0.0 0.000116
1 0.0 0.001989
2 0.0 0.020810
3 0.0 0.134725
4 0.0 0.521703
5 0.0 0.000000
----oT
Episode 8: total_steps = 5
left right
0 0.0 0.000283
1 0.0 0.003663
2 0.0 0.030854
3 0.0 0.168206
4 0.0 0.569533
5 0.0 0.000000
----oT
Episode 9: total_steps = 5
left right
0 0.0 0.000585
1 0.0 0.006073
2 0.0 0.042907
3 0.0 0.202643
4 0.0 0.612580
5 0.0 0.000000
----oT
Episode 10: total_steps = 5
left right
0 0.0 0.001073
1 0.0 0.009328
2 0.0 0.056855
3 0.0 0.237511
4 0.0 0.651322
5 0.0 0.000000
----oT
Episode 11: total_steps = 5
left right
0 0.0 0.001805
1 0.0 0.013512
2 0.0 0.072545
3 0.0 0.272379
4 0.0 0.686189
5 0.0 0.000000
----oT
Episode 12: total_steps = 5
left right
0 0.0 0.002840
1 0.0 0.018690
2 0.0 0.089805
3 0.0 0.306898
4 0.0 0.717570
5 0.0 0.000000
----oT
Episode 13: total_steps = 5
left right
0 0.0 0.004239
1 0.0 0.024903
2 0.0 0.108445
3 0.0 0.340790
4 0.0 0.745813
5 0.0 0.000000
----oT
Episode 14: total_steps = 8
left right
0 0.000381 0.007692
1 0.000545 0.032173
2 0.000000 0.128272
3 0.000000 0.373834
4 0.000000 0.771232
5 0.000000 0.000000
----oT
Episode 15: total_steps = 5
left right
0 0.000381 0.009818
1 0.000545 0.040500
2 0.000000 0.149089
3 0.000000 0.405861
4 0.000000 0.794109
5 0.000000 0.000000
----oT
Episode 16: total_steps = 5
left right
0 0.000381 0.012481
1 0.000545 0.049868
2 0.000000 0.170708
3 0.000000 0.436745
4 0.000000 0.814698
5 0.000000 0.000000
----oT
Episode 17: total_steps = 5
left right
0 0.000381 0.015721
1 0.000545 0.060245
2 0.000000 0.192944
3 0.000000 0.466393
4 0.000000 0.833228
5 0.000000 0.000000
----oT
Episode 18: total_steps = 5
left right
0 0.000381 0.019571
1 0.000545 0.071585
2 0.000000 0.215625
3 0.000000 0.494744
4 0.000000 0.849905
5 0.000000 0.000000
----oT
Episode 19: total_steps = 5
left right
0 0.000381 0.024057
1 0.000545 0.083833
2 0.000000 0.238590
3 0.000000 0.521762
4 0.000000 0.864915
5 0.000000 0.000000
----oT
Episode 20: total_steps = 7
left right
0 0.000381 0.029196
1 0.000545 0.096923
2 0.000000 0.282479
3 0.023552 0.547428
4 0.000000 0.878423
5 0.000000 0.000000
Q-table:
left right
0 0.000381 0.029196
1 0.000545 0.096923
2 0.000000 0.282479
3 0.023552 0.547428
4 0.000000 0.878423
5 0.000000 0.000000
todo
儲存結果
將上述的 Dataframe儲存
應用
載入上述儲存的結果,套用在新的狀態
結論
Q-Learning 就是學習(記錄)前人的經驗,然後判斷最佳的解決方式
參考
https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/general-rl
https://ithelp.ithome.com.tw/articles/10234568
