tensorflow 有些常用的函數,需要仔細的背起來
tf.random.normal
標準常態分佈亂數會在大部份集中於0左右的小數亂數。其實np.random.normal()也可以產生此功能。
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import tensorflow as tf
import pylab as plt
import seaborn as sns
batch=10000
x=tf.random.normal([batch])
y=tf.random.normal([batch])
#plt.scatter(x, y, s=0.1)
sns.histplot(x)
plt.savefig("tf_normal_histplot.jpg")
plt.show()
plt點散圖如下
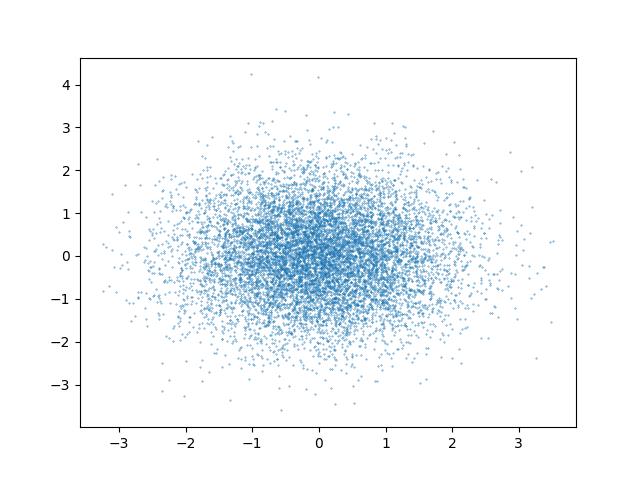
海生圖如下
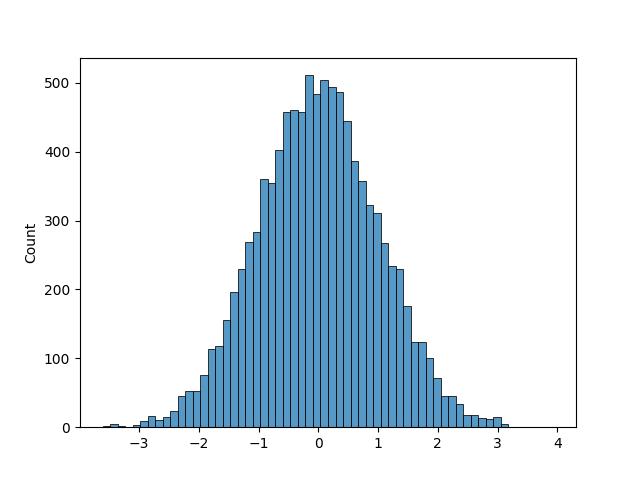
tf.random.uniform
在 陣列 這篇的說明,有提到 tf.random.uniform是產生均勻分佈陣列的函數,參數只需傳入要產生亂數的數量即可。另外 tf.random.unifomr 還可以下達 minval 及 maxval 設定最小值及最大值,但不包含最大值。
底下代碼可以產生均勻分佈亂數
import os os.environ['TF_CPP_MIN_LOG_LEVEL']='2' import numpy as np import tensorflow as tf import pylab as plt import seaborn as sns batch=10000 x=tf.random.uniform([batch])
y=tf.random.uniform([batch]) plt.scatter(x, y, s=0.1) #sns.histplot(y) print(y.numpy()) plt.savefig("tf_uniform_scatter.jpg") plt.show()
plt點散圖如下
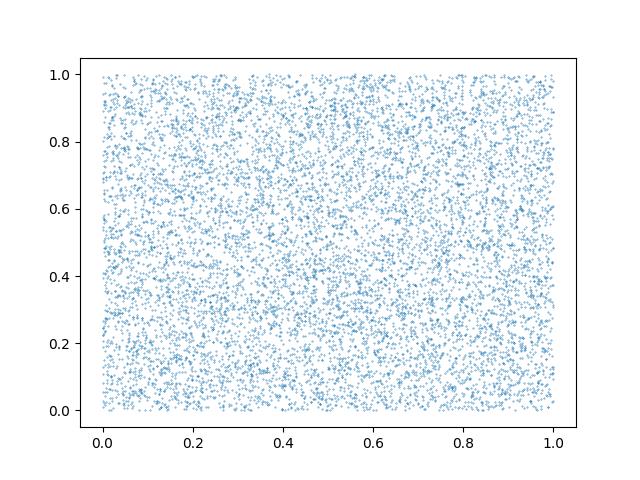
海生圖分佈狀態如下
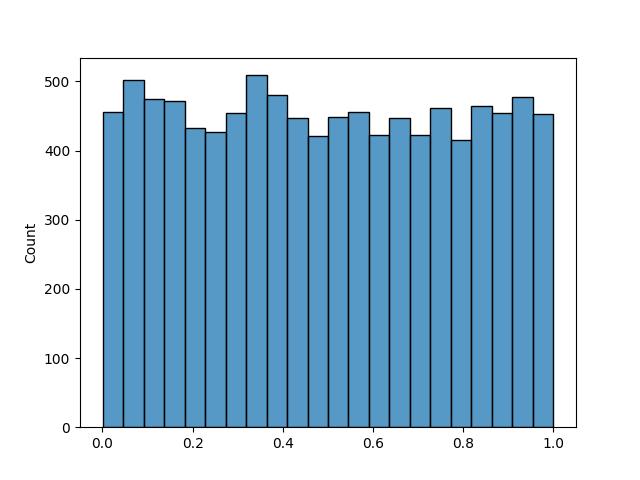
產生均勻分佈亂數,其實也可以用 np. random.uniform(0, 1, batch)。這二個有什麼不同呢? 當產生的數量多達1億個的時候,這二個所花費的時間差不多是在 0.4 秒左右,但如果產生的數量大於 1 億,numpy 的效能就會遠遠落後 tf 很多。
import os import time os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' import tensorflow as tf import numpy as np batch=500_000_000 t1=time.time() a=tf.random.uniform([batch]) t2=time.time() print(f'tf花費 : {t2-t1}秒') t1=time.time() b=np.random.uniform(0, 1, batch) t2=time.time() print(f'np花費 : {t2-t1}秒')
結果 : tf花費 : 0.4383711814880371秒 np花費 : 2.5611190795898438秒
tf.sqrt
sqrt 為求取平方的函數,只能用於小數型態。如果是整數型態,會發生例外錯誤。
另外如果傳入的型態是陣列的話,就會將陣列中的每一個元素進行運算。
import os os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' import tensorflow as tf #tf.sqrt只能用在小數型態 a=tf.constant(10.) print(tf.sqrt(a)) #底下為整數型態,無法使用 sqrt #b=tf.constant(10) #print(tf.sqrt(b)) c=tf.constant([1., 2., 3.]) print(tf.sqrt(c)) 結果 : tf.Tensor(3.1622777, shape=(), dtype=float32) tf.Tensor([1. 1.4142135 1.7320508], shape=(3,), dtype=float32)
numpy 也有 np.sqrt 的方法,底下對 1 億個數字進行進算,可見 tf.sqrt 效能遠遠比 numpy 好很多
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
import numpy as np
import time
batch=100_000_000
t1=time.time()
a=tf.random.uniform([batch])
t2=time.time()
print(f'tf產生亂數花費 : {t2-t1}秒')
t1=time.time()
b=np.random.uniform(0, 1, batch)
t2=time.time()
print(f'np產生亂數花費 : {t2-t1}秒')
t1=time.time()
a=tf.sqrt(a)
t2=time.time()
print(f'tf計算平方花費 : {t2-t1}秒')
t1=time.time()
b=np.sqrt(b)
t2=time.time()
print(f'np計算平方花費 : {t2-t1}秒')
結果:
tf產生亂數花費 : 0.44187140464782715秒
np產生亂數花費 : 0.5215818881988525秒
tf計算平方花費 : 0.0009970664978027344秒
np計算平方花費 : 0.14860248565673828秒
tf.square
tf.square為求取平方值,適用於整數及小數。同樣如果是陣列,也會足一將每個元素的平方計算一遍。
import os os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' import tensorflow as tf a=tf.constant(10.) print(tf.square(a)) b=tf.constant(10) print(tf.square(b))
結果 : tf.Tensor(100.0, shape=(), dtype=float32) tf.Tensor(100, shape=(), dtype=int32)
tf.where
where後面的參數為條件,此法可將陣列中符合條件的索引值集合成一個新的 n*1 的 Tensor 陣列。
如果要取出符合的值,需使用 value = tf.gather(x, idx)。
最後若要得知符合的數量,使用 value.shape[0]。
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
batch=10
x=tf.random.uniform([batch])
print(f'原始資料 : {x}')
idx=tf.where(x<=0.5)
print(f'符合的索引 :\n{idx}')
value=tf.gather(x, idx)
print(f'符合的值 : {value}')
print(f'符合的數量 : {value.shape[0]}')
原始資料 : [0.5912652 0.97370183 0.21289659 0.52576315 0.13146174 0.76325166
0.10665309 0.54943335 0.59710836 0.76287985]
符合的索引 :
[[2]
[4]
[6]]
符合的值 : [[0.21289659]
[0.13146174]
[0.10665309]]
符合的數量 : 3
導數
導數就是微分,微分就是導數。比如$(f(x)=x^{2})$,經過一次微分後,結果為$(f'(x)=2x)$,所以當x=3時,$(y=f'(x)=6)$
with tf.GradientTape() as prototype 的區塊中,就是在宣告函數的原型。然後再使用y_grad=prototype.gradient(x, y)就可以求取y對x的導數。
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import tensorflow as tf
cpus=tf.config.experimental.list_physical_devices(device_type='CPU')
tf.config.set_visible_devices(devices=cpus)
x = tf.Variable(3.)
with tf.GradientTape() as prototype:#宣告原型函數
y = tf.pow(x, 2)
y_grad = prototype.gradient(y, x)# 計算y關於x的導數
print('y=x^2, x=3, y=',y)
print('一次微分後,y導數=', y_grad)
結果 :
y=x^2, x=3, y= tf.Tensor(9.0, shape=(), dtype=float32)
一次微分後,y導數= tf.Tensor(6.0, shape=(), dtype=float32)
損失函數偏導數
$(x=\begin{bmatrix}1 & 2\\ 3 & 4 \end{bmatrix})$ , $(y=\begin{bmatrix}1\\2\end{bmatrix})$ , $(w=\begin{bmatrix}1\\2\end{bmatrix})$ , $(b=1)$
假設 y=xw + b ,則底下為其損失函數
$(L(w, b)=\sum (xw+b-y )^{2})$
import tensorflow as tf
X = tf.constant([[1., 2.], [3., 4.]])
y = tf.constant([[1.], [2.]])
w = tf.Variable(initial_value=[[1.], [2.]])
b = tf.Variable(initial_value=1.)
with tf.GradientTape() as tape:
L = tf.reduce_sum(tf.square(tf.matmul(X, w) + b - y))
w_grad, b_grad = tape.gradient(L, [w, b]) # 計算L(w, b)關於w, b的偏導數
print(L)
print(w_grad)
print(b_grad)
結果:
tf.Tensor(125.0, shape=(), dtype=float32)
tf.Tensor(
[[ 70.]
[100.]], shape=(2, 1), dtype=float32)
tf.Tensor(30.0, shape=(), dtype=float32)
todo
