卡迪兒座標系(Cartesian coordinate system)

我們常稱的xy座標，或是xyz立体空間座標，就是卡迪兒座標系，這傢伙是法國人。由二個或三個正交線所組成的。如下圖為3D立体座標系。

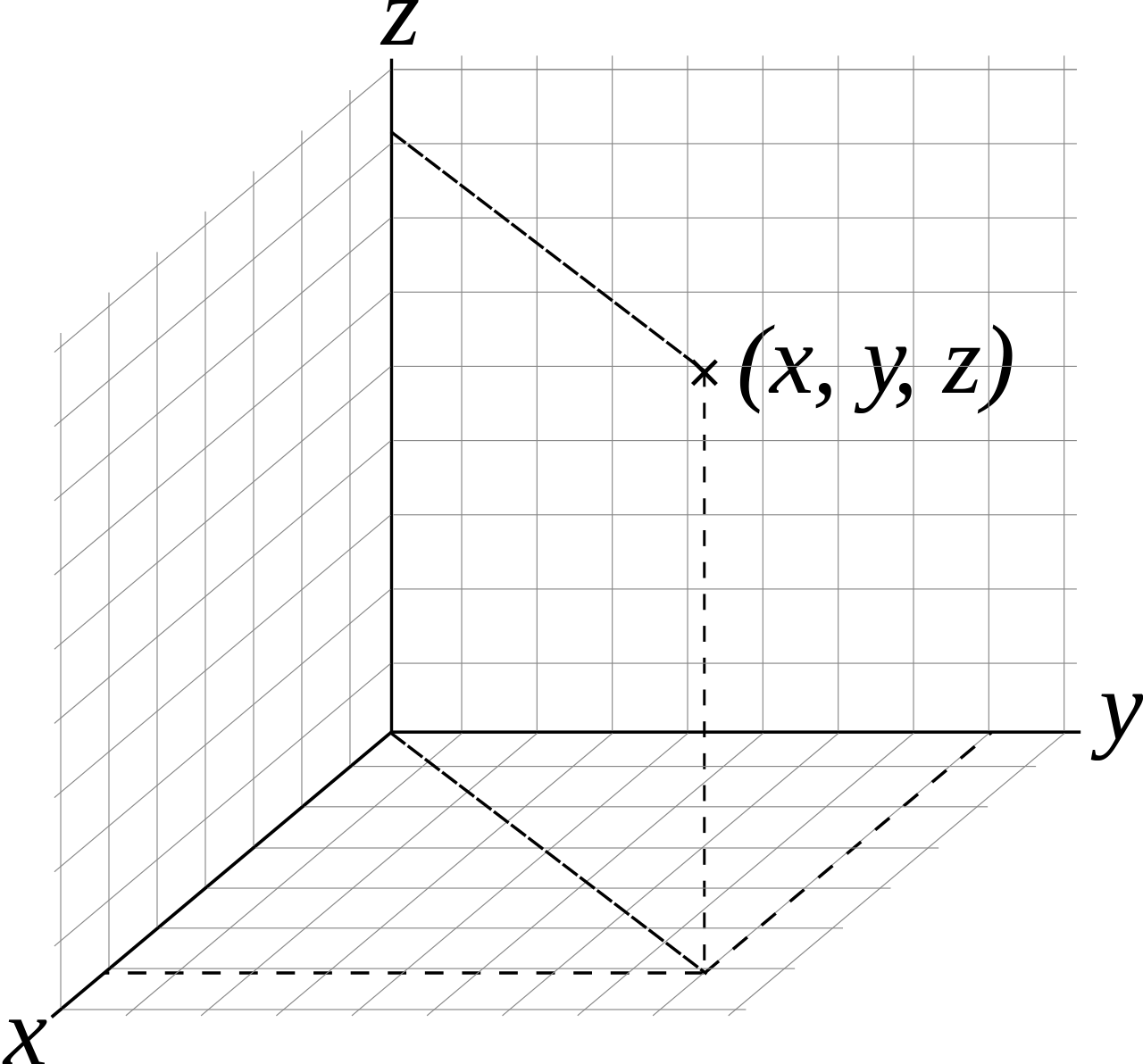
三角函數

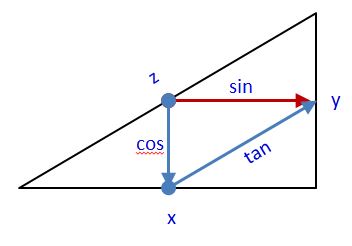
$(sin\theta =\frac{y}{z})$

$(cos\theta =\frac{x}{z})$

$(tan\theta =\frac{y}{x})$

三角面積 : $(\frac{x*y}{2})$

反三角函數 : $(sin^{-1}(\frac{y}{z}))$=角度

弧度(弳度) : $(1^{o}=\frac{\pi}{180})$

圓公式

圓周 : $(2\pi r)$
圓面積 : $(\pi r^{2})$
正弦波 : $(f(x)=A*sin(k\pi t))$ : A為振幅，k 為波峰數，t 為時間

圓函數

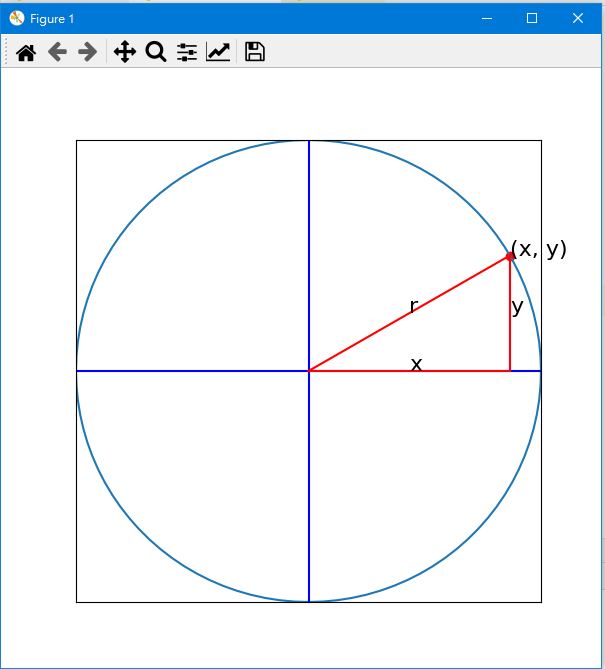
上述的圖形，由下面的Python代碼所繪製而成的。(x, y)座標點中，x, y分別為

$(x=r*cos(\frac{\pi}{180}*\theta))$
$(y=r*sin(\frac{\pi}{180}*\theta))$

當$(\theta)$ 由 0變換到360度時，即形成一個圓

import numpy as np
import pylab as plt
r=10
n=100
x=[]
y=[]
for i in range(n+1):
    angle=360/n*i
    x.append(r*np.cos(np.pi/180*angle))
    y.append(r * np.sin(np.pi / 180 * angle))
plt.figure(figsize=(6,6))
plt.xticks([])
plt.yticks([])
plt.plot(x, y)
plt.xlim(-r, r)
plt.ylim(-r, r)
plt.plot([-r, r],[0, 0], color='blue')#畫X軸
plt.plot([0, 0],[-r, r], color='blue')#畫y軸
#底下畫個三角型
x1=r*np.cos(np.pi/180*30)
y1=r*np.sin(np.pi/180*30)
plt.scatter([x1],[y1], color='red')#畫點
plt.text(x1, y1,s='(x, y)', fontsize=16)
plt.text(x1/2,0 ,s='x', fontsize=16)
plt.text(x1, y1/2 ,s='y', fontsize=16)
plt.text(x1/2, y1/2 ,s='r', fontsize=16)
plt.plot([x1, x1],[0, y1], color='red')
plt.plot([0, x1],[0, y1], color='red')
plt.plot([0, x1],[0, 0], color='red')

plt.show()