馬可夫決策比馬可夫鍊多了一個狀態，底下以 4*4 的格子作為說明

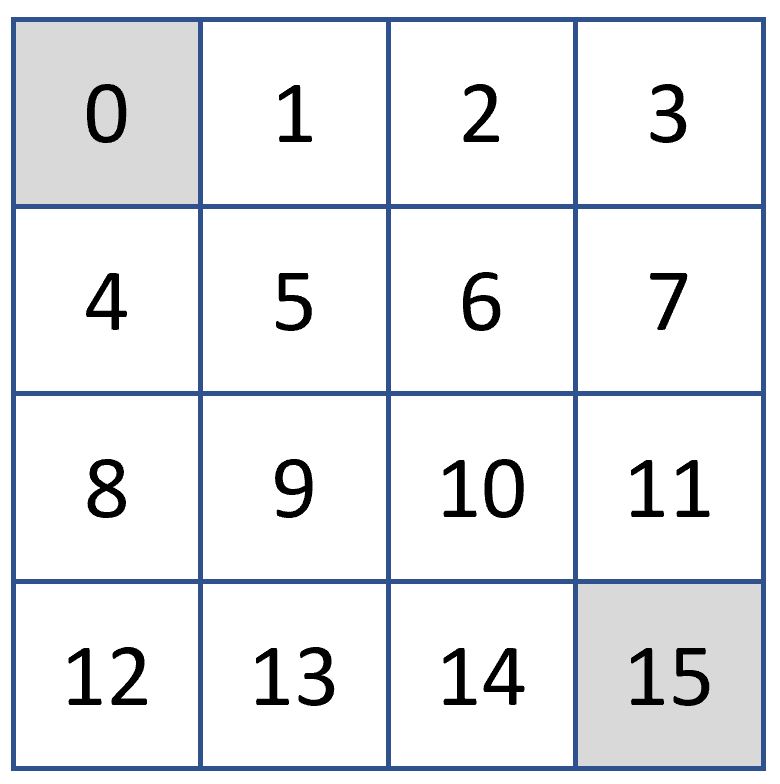
上述的格子中，共有 0~15 種狀態，0 及 15 為最終點。一開始，我們可能位於 0~15 其中一種狀況，比如一開始位於 5 的地方。而移動的方式只有四種，分別是上、下、左、右，沒有左上、左下、右上、右下。那麼怎麼由 5 走到 0 呢? 可能的方式有 5 -> 1 -> 0，5 -> 4 -> 0，5 -> 6 ->2 -> 1 -> 0，……..。

數學模型

底下使用統計學的數學模型定義各種名詞

狀態集(State sets) : $(S=\{s_{0}, s_{1}, …., s_{m}\})$，上述為$(S=\{0, 1, 2,  …., 15\})$
初始狀態(Initial state) : $(s_{5})$ ，上述為 5
動作集(Action sets) : $(A=\{a_{0}, a_{1}, …., a_{n}\})$，上述為 $(A=\{上, 下, 左, 右\})$
轉移模型(Transition model) : T(s, a, s’)，比如 T(5, 上, 1)
獎勵函數(Reward function) : 評價決策的結果好或不好

策略$(\pi)$

將狀態與動作對應到機率的函數。表示某種狀態下，採取某種動作的機率，記做 $(\pi(a|s))$

np.npy

.npy 檔是利用 numpy 的 save將陣列儲存在碟碟裏，待下次需要時，再用 np.load 將檔案載入到記憶体中

T.npy

4*4 格的狀況，分別是 0~15 種(每種狀態用1個數字描述，稱為數位化)。t.npy 檔為 16 *16 *4 的型態，分別記錄由某一狀態 (行) 切換到另一狀態 (列) 時，可執行的動作 (切換後的狀態16種 * 原本的狀態16種 * 可動作集 4 種)。比如由 1 狀態切到 2 狀態 ，可執行的動作為 {0,0,0,1} =>{上, 左, 下, 右}，所以右為 1，其它為 0

import numpy as np
T = np.load('./T.npy')
for i in range(16):
    for j in range(16):
        print(f'{j} - > {i} : {T[i][j]}')
結果 : 
15 - > 1 : [0. 0. 0. 0.]
0 - > 2 : [0. 0. 0. 0.]
1 - > 2 : [0. 0. 0. 1.]
2 - > 2 : [1. 0. 0. 0.]
3 - > 2 : [0. 1. 0. 0.]
4 - > 2 : [0. 0. 0. 0.]
5 - > 2 : [0. 0. 0. 0.]
6 - > 2 : [1. 0. 0. 0.]

todo