特徵就是某個點(事件)的維度, 比如有 4 個點，分別為 A點(10,15,20)，B點(10,15,60)，C點(12, 10,15)，D點(11, 15, 20)。那麼 A 跟 (B, C, D) 這三點那個最接近呢?

這就要先算 AB ，AC ，AD 這 3 個的距離。那個比較短就是答案。

todo

少點(圖)多維度(像素) => 多點(圖)少維度 (像素)

二維

如下圖所示，二維空間中紅色的點，可以串連成一條藍色曲線

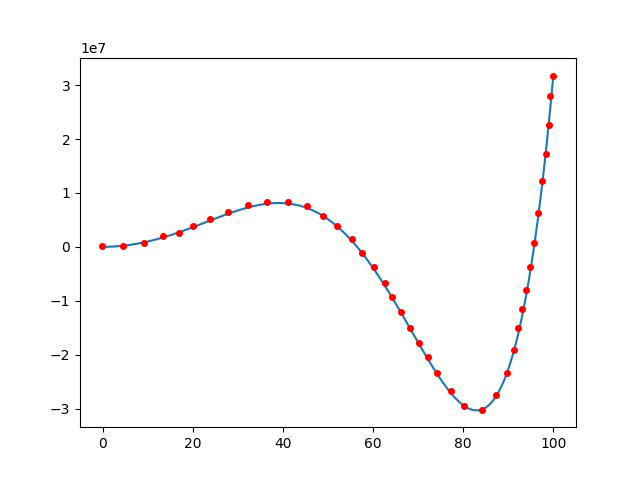
每個紅點之間，若想多增加一個點，可以由 $(y=0.001x^6-0.1x^5-0.68x^4+10000x^2+2)$ 算出來。

這個圖只有一個變數(特徵)，就是 x ，而 y 是結果。

物理特性

比如 x 軸如果是 5 cm，y 軸為 3; x 軸如果是10 cm，y 軸為 2 cm

又比如天氣，(濕度)=(下雨機率)，(50)=(20%)，(80)=(90%)

在三維空間中，x 軸及 y 軸決定 z 軸的高度，公式可能是 $(z= ax^6+by^6+cx^5+dx^4-ey^3….)$

x 及 y 決定 z 的值， z 值可以由公式 $(z= ax^6+by^6+cx^5+dx^4-ey^3….)$ 算出。所以三維空間中，只有二個特徵 (x, y )

比如 (x, y) 是 (10m, 5m) ，z 為 50m。又如 (11m, 6m)， z 是55m。
又比如天氣 (節氣, 濕度) = (下雨機率)，(清明,50)=(90%), (清明,70)=(100%)，(夏至, 70) = (0%)

因為清明時節雨紛紛，而夏至是白晝最長的一天，悶熱不常下雨。

todo

向量是為了解釋三維以上的事，因為三維以上無法用圖來表答，所以就用向量(特徵) 這個名詞表示維度，然後計算其結果。