網路上那麼多的動態規化教學，總是一大堆看不懂的東西，本篇先使用付款實例，進行不同的方式說明

付款實例

台灣的幣別有 1, 5, 10, 50, 100, 500, 1000 等 7 種幣別。

如果你消費了 987 元，那應該怎麼付錢，才能淘出最少數量的貨幣數量付給店家足夠的金額 ? 我們腦袋隨便一算，很容易的就知道要付 1 張 500 元，4 張 100 元，1 個 50元，3 個 10 元，1 個 5 元，2 個 1 元，總共是 1+4+1+3+1+2 = 12 個貨幣。

如果我們的貨幣 (狀態) 有上百種，那該如何用電腦算出最少的數量呢 ????
請特別注意，我們的要求，是如何付出最少的貨幣數量，當然金額一定要足夠。

思考邏輯

假設我們要付987元，那麼可以有如下選擇方案 — (付1元剩 986元)，(付5元剩 982元)，(付10元剩 977元)，(付50元剩 937元)，(付100元剩 887元)，(付500元剩 487元)，共六種方式。每一種付款方式，剩餘的金額分別為 (986, 982, 977, 937, 887, 487) ，而這些錢的付款最少次數以前就算過了(都是11次)。

所以就是(12,12,12,12,12,12)次，然後從這個集合中選取最小值。

上述 (986,982,977,937,887,487)  這些付款方式的最佳解，怎麼就以前就解過了呢? 原來是用 for 迴圈，從1塊錢，2塊錢，一直堆積上來，並儲存在記憶体中的。

總付款 : 987元
貨幣(一次)    剩餘         總共
1            986(11次)    11+1=12次
5            982(11次)    11+1=12次
10           977(11次)    11+1=12次
50           937(11次)    11+1=12次
100          887(11次)    11+1=12次
500          487(11次)    11+1=12次

實際代碼

底下是實際的完整代碼，最後顯示的結果是 12 種。

import collections
import math
def pay(coins, amount):
    dp = collections.defaultdict(lambda: float("inf"))
    dp[0] = 0
    for i in range(1, amount + 1):
        print(f'amount : {i} => {[1 + dp[i - coin] for coin in coins]} =>', end="")
        dp[i] = min([1 + dp[i - coin] for coin in coins])
        print(dp[i])
    return -1 if math.isinf(dp[amount]) else dp[amount]
print(pay([1,5, 10, 50，100,500,1000], 987))
結果 :
amount : 985 => [18, 14, 14, 14, 14, inf] =>14
amount : 986 => [15, 15, 15, 15, 15, inf] =>15
amount : 987 => [16, 16, 16, 16, 16, inf] =>12
12

動態規畫，就是從舊有經驗所取得的最佳解，然後獲取未來的解法。

方格移動

在一個 m*n 的格子中，從左上角 (0, 0) 走到右下角 (m-1, n-1) 共有幾種方式呢。這邊有個規定，只能往右邊或往下面走，不可以斜著走，也不可以往上往左走。

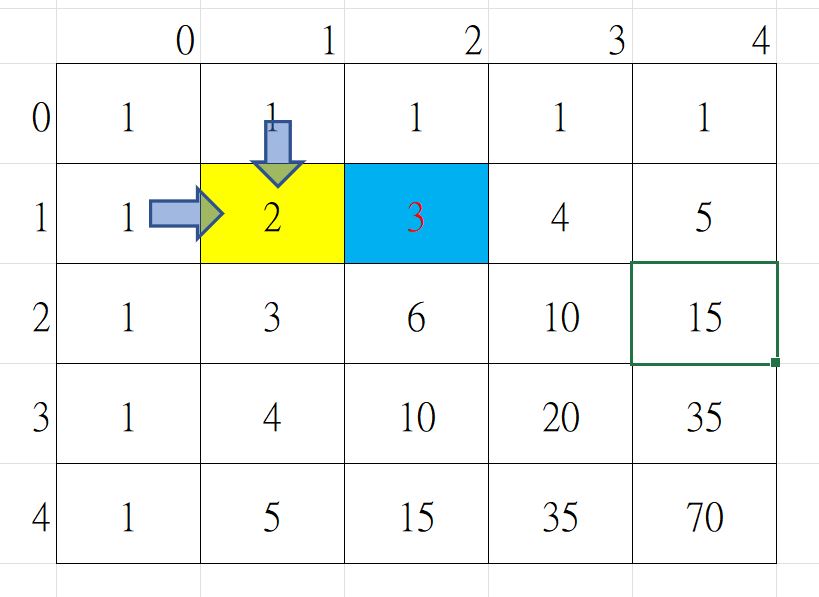
上圖要走到黃色那格(1，1)，可能由 (0, 1) 往下走，也可能由(1, 0)往右走，所以要走到黃色格有2種方式。那要走到藍色那格有幾種方式呢，就是 (1, 1) 的2種方式+ (0,2) 的 1 種方式 = 3 種方式。

如此依序往右往下計算每一個，直到最右下角就是70種方式。

import numpy as np
def paths(m, n):
    # 先開一個 m*n 的大表格，並讓邊界的預設值為 1（代表有一種走法）。
    dp=np.ones([m,n], dtype=np.int32)
    for row in range(1, m):
        for col in range(1, n):
            dp[row][col] = dp[row-1][col] + dp[row][col-1]
    return dp[m-1][n-1]
print(paths(5,5))
結果 :
70

最大正方型面積

在一個 m*n 的格子中，1表示土地，0表示海洋，那麼如何計算最大的正方型土地面積呢? 下圖是矩陣的型狀。

>

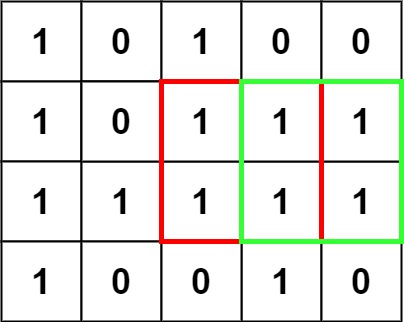底下是完整的程式碼

def maximalSquare(matrix):
    #map會根據指定的函數，對每個list裏的元素進行運算
    #比如 map(lambda x:x**x, [1,2,3,4])
    arr = [list(map(int, row)) for row in matrix]
    print(arr)
    for i in range(1, len(arr)):
        for j in range(1, len(arr[i])):
            arr[i][j] = min(arr[i-1][j], arr[i][j-1], arr[i-1][j-1]) + 1 if arr[i][j] == 1 else 0
    print(arr)
    return max([max(row) for row in arr], default=0) ** 2
matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
print(maximalSquare(matrix))
結果 :
[[1, 0, 1, 0, 0], [1, 0, 1, 1, 1], [1, 1, 1, 1, 1], [1, 0, 0, 1, 0]]
[[1, 0, 1, 0, 0], [1, 0, 1, 1, 1], [1, 1, 1, 2, 2], [1, 0, 0, 1, 0]]
4

動態規畫其實是一門很深的課程，差不多需一學期(6個月)的時間來學習，裏面有很多的演算法可以應用。有興趣的人可以參考如下卡卡恩大神所寫的文章.

https://ithelp.ithome.com.tw/articles/10215363