底下使用迷宮的走法,走到 (1,2) 或 (2, 1) 為地獄,得 -1分,走到 (2,2) 為天堂,得 1 分。本例使用 tkinter 繪製方格。
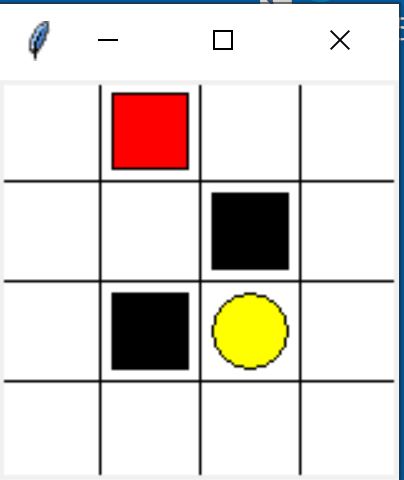
Q-Learning 應用在此例,計算每一格往[上,下,左,右] 四個方向的分數,公式與上一篇相同
$(Q(s,a)=Q(s,a)+lr[r+\gamma*maxQ(s’)-Q(s,a)])$
Q 表一樣是二維表格,但每列有四行資料
上 下 左 右 (0, 0) 0.0 0.0 0.0 0.0 (0, 1) 0.0 0.0 0.0 0.0 (1, 1) 0.0 0.0 0.0 0.0 terminal 0.0 0.0 0.0 0.0
主程式
主程式如下
from Brain import Brain
from Maze import Maze
import pandas as pd
def update():
for epoch in range(100):
#初始化 state 觀測值
s = maze.reset()
while True:
#更新 tkinter
maze.render()
# RL 依 state 觀測值選取動作
action = rl.choose_action(str(s))
# RL 執行動作後,取得一下個狀態觀測值、回報值,並檢查是否完成(掉入天堂或升上天堂)
s_next, reward, done = maze.step(action)
# RL 從 (狀態, 動作, 回報值) 學習
rl.learn(str(s), action, reward, str(s_next))
# 轉換到下一個狀態
s = s_next
# 進入地獄或天堂就中止
if done:
break
print(f'epoch : {epoch}')
print(f"=====================final table=====================")
df=pd.DataFrame(
{"up":rl.table[0],
"down":rl.table[1],
"left":rl.table[2],
"right":rl.table[3],
"max":rl.table.max(axis=1)
},
index=rl.table.index
)
print(df)
maze.destroy()
if __name__ == "__main__":
maze = Maze()
rl = Brain(actions=list(range(4)))
#rl=Brain()
maze.after(100, update)
maze.mainloop()
繪製迷宮
迷宮繪製程式如下,Maze.py
import random
import threading
import time
import tkinter as tk
import numpy as np
cols=4#4行
rows=4#4列
unit=80#每格40像素
gap=5
class Maze(tk.Tk):
def __init__(self):
super().__init__()
#產生一個畫布
self.canvas=tk.Canvas(
self,
bg='white',
width=cols*unit,
height=rows*unit
)
self.center=np.array([unit//2, unit//2])
#垂直線
for x in range(0, cols*unit, unit):
self.canvas.create_line(x, 0, x, rows*unit)
#水平線
#水平線
for y in range(0, rows*unit, unit):
self.canvas.create_line(0, y, cols*unit, y)
self.hell1=self.rectangle(2,1,"black")
self.hell2 = self.rectangle(1, 2, "black")
self.heaven=self.oval(2,2,"yellow")
self.rect=self.rectangle(0,0,'red')
self.canvas.pack()#最後一定要 pack,才會顯示圖形
self.reset()
# self.thread=threading.Thread(target=self.rnd)
# self.thread.start()
def reset(self):
time.sleep(0.02)
self.canvas.delete(self.rect)
self.rect=self.rectangle(0,0,"red")
self.update()
return 0,0
def render(self):
time.sleep(0.01)
self.update()
def step(self, action):
x1, y1, x2, y2=self.canvas.coords(self.rect)#取得矩型的左上及右下座標
#mx : x軸的移動距離
#my : y軸的移動距離
mx, my = 0, 0
if action==0:#往上
if y1>unit:#s[0]紅色左上角的x值,s[1]紅色左上角的 y 值
my -= unit
elif action==1:#往下
if y1<(rows-1)*unit:
my += unit
elif action==2:#往左
if x1>unit:
mx -= unit
elif action==3:#往右
if x1<(cols-1)*unit:
mx += unit
self.canvas.move(self.rect, mx, my)
s_next=self.canvas.coords(self.rect)
#計算回報值
if s_next == self.canvas.coords(self.heaven):
reward = 1#到天堂的回報值為 1
done=True
s_next='terminal'
elif s_next in [self.canvas.coords(self.hell1), self.canvas.coords(self.hell2)]:
reward = -1#到地獄的回報值為 -1
done=True
s_next = 'terminal'
else:
#s_next(row, col)
s_next = (int(s_next[1]/unit), int(s_next[0]/unit))
reward=0
done=False
time.sleep(0.01)
return s_next, reward, done
def coordinate(self, x, y):
c=self.center+np.array([x*unit, y*unit])
return c[0]-(unit//2-gap), c[1]-(unit//2-gap), c[0]+(unit//2-gap), c[1]+(unit//2-gap)
def rectangle(self,x, y, color):
x1, y1, x2, y2 = self.coordinate(x, y)
return self.canvas.create_rectangle(x1, y1, x2, y2, fill=color)
def oval(self, x, y, color):
x1, y1, x2, y2 = self.coordinate(x, y)
return self.canvas.create_oval(x1, y1, x2, y2, fill=color)
#底下是動畫用的
def rnd(self):
while True:
x=random.randint(0, cols-1)
y=random.randint(0, rows-1)
self.canvas.delete(self.rect)
self.rect=self.rectangle(x, y, "red")
self.update()
time.sleep(0.02)
強化學習
強化學習 Brain.py 如下
import pandas as pd
import numpy as np
class Brain():
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
#以下是在 main 中自已定的 0:up, 1:down, 2:left, 3:right
self.actions=actions#[0,1,2,3]
self.lr=learning_rate
self.gamma=reward_decay
self.epsilon=e_greedy
self.table=pd.DataFrame(columns=self.actions, dtype=np.float64)
def choose_action(self, s):
self.check_state_exits(s)
if np.random.uniform()<self.epsilon:#驗証
state_action=self.table.loc[s,:]
action=np.random.choice(state_action[state_action==np.max(state_action)].index)
else:#隨機選取上下左右的動作
action=np.random.choice(self.actions)
return action
def q_value(self, s, action, reward, s_next):
self.check_state_exits(s_next)
if s_next != 'terminal':
target=reward + self.gamma*self.table.loc[s_next,:].max()
else:
target=reward
self.table.loc[s,action]+=self.lr*(target-self.table.loc[s, action])
def check_state_exits(self,s):
if s not in self.table.index:
s=pd.Series(
[0]*len(self.actions),
index=self.table.columns,
name=s,
)
self.table=pd.concat([self.table, pd.DataFrame(s).T])#T置轉90度,也就是直向變橫向
print("==============新狀態===============")
print(self.table)
最後結果
在 final table 藍色的部份就是下一步要走的方向
epoch : 0
=====================新狀態=====================
0 1 2 3
(0, 0) 0.0 0.0 0.0 0.0
=====================新狀態=====================
0 1 2 3
(0, 0) 0.0 0.0 0.0 0.0
(1, 0) 0.0 0.0 0.0 0.0
=====================新狀態=====================
.......
epoch : 99
=====================final table=====================
up down left right max
(0, 0) 5.266589e-11 4.782969e-17 1.204786e-06 1.480376e-04 1.480376e-04
(0, 1) 1.169576e-05 1.801575e-08 0.000000e+00 1.194645e-03 1.194645e-03
(1, 1) 3.280616e-06 -1.990000e-02 0.000000e+00 -1.990000e-02 3.280616e-06
terminal 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
(1, 0) 0.000000e+00 0.000000e+00 0.000000e+00 1.779782e-09 1.779782e-09
(0, 2) 1.864988e-05 -5.851985e-02 6.778068e-07 8.050405e-03 8.050405e-03
(0, 3) 0.000000e+00 4.487453e-02 4.985308e-06 3.576159e-04 4.487453e-02
(2, 0) 0.000000e+00 0.000000e+00 0.000000e+00 -2.970100e-02 0.000000e+00
(1, 3) 3.222018e-04 1.898110e-01 -1.990000e-02 5.586076e-04 1.898110e-01
(2, 3) 2.864037e-03 0.000000e+00 5.657687e-01 2.668971e-03 5.657687e-01
(3, 0) 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
(3, 1) -1.000000e-02 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
(3, 2) 1.000000e-02 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e-02
(3, 3) 4.721940e-03 0.000000e+00 0.000000e+00 0.000000e+00 4.721940e-03
上述藍色的部份,表示如果一開始位於 (0,0) 的位置,基於選擇最大值的原則,最佳走法為 :
(0,0) -> 往右(0,1) -> 往右(0,2) -> 往右(0,3) -> 往下(1,3) -> 往下(2,3) -> 往左(2,3)
參考 : https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/tabular-q1
