機器學習與深度學習

深度學習是屬於機器學習其中一個分支，深度學習不需要輸入特徵，會自已去找特徵。

不過此房價預測範例必需輸入特徵，所以不屬於深度學習範圍。那為何把此專案例入深度學習呢??

在此必需承認一件事，前面的 AI人工智慧章節混合了 “非深度學習” 及 “深度學習” 的課程。如今新增了深度學習的課程，所以必需強加區隔。在以往的 AI人工智慧並未介紹如何由特徵進行分析，所以由此開始介紹。

波士頓房價預測

盡管我們對房價不是那麼的關心 (就買不起咩)，更何況這是波士頓的房價狀況。但這一道題目是許多機器學習者的起手式，介紹了資料處理的詳細步驟，所以必需耐心理解。

心理準備

每個人都希望藉由 AI 來精準預測結果，這是外行人的想法，說的更難聽一點，這是腦殘人的想法。

房價會依賣方的心情(吸毒急需錢，戰爭要移民……..)，買方的心情(財力，需求…….)，通膨，物價指數，有上千萬種因素。而且房價不是用斤兩來秤的，也不是一斤多少錢有絕對的標準，所以別再問為什麼預測的房價不一樣(或不準)，因為這只是一個大略的範圍而以。

載入資料

首先由 scikit-learn load_boston()載入波士頓房價資料，請先安裝scikit-learn 1.1.3 套件。請注意，scikit-learn 自 1.2 開始就把波士頓房價移除了，所以要安裝舊版的 1.1.3 版。

pip install scikit-learn==1.1.3 matplotlib seaborn

然後使用如下代碼載入資料

from sklearn.datasets import load_boston
boston_dataset = load_boston()
print(boston_dataset.data.shape)
print(boston_dataset.DESCR)#列出每項特徵的說明

boston_dataset 為一字典格式，data 為每間房子的特徵，共有506筆資料，13個特徵。target為每間房子的房價。feature_names是每間房子的特徵名稱。DESCR是每個特徵的說明。

轉成DataFrame

將boston_dataset.data轉成DataFrame格式 df ，再於最前面加入”PRICE”欄位，其值為 boston_dataset.target 房價。

display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
df=pd.DataFrame(data=boston_dataset.data, columns=boston_dataset.feature_names)
df.insert(0, column="PRICE", value=boston_dataset.target)
print(df)
結果:
     PRICE      CRIM     ZN  INDUS  CHAS     NOX     RM    AGE      DIS   RAD    TAX  PTRATIO       B  LSTAT
0     24.0   0.00632   18.0   2.31   0.0  0.5380  6.575   65.2   4.0900   1.0  296.0     15.3  396.90   4.98
1     21.6   0.02731    0.0   7.07   0.0  0.4690  6.421   78.9   4.9671   2.0  242.0     17.8  396.90   9.14
2     34.7   0.02729    0.0   7.07   0.0  0.4690  7.185   61.1   4.9671   2.0  242.0     17.8  392.83   4.03
3     33.4   0.03237    0.0   2.18   0.0  0.4580  6.998   45.8   6.0622   3.0  222.0     18.7  394.63   2.94
4     36.2   0.06905    0.0   2.18   0.0  0.4580  7.147   54.2   6.0622   3.0  222.0     18.7  396.90   5.33
5     28.7   0.02985    0.0   2.18   0.0  0.4580  6.430   58.7   6.0622   3.0  222.0     18.7  394.12   5.21
....................................

EDA(Explorator Data Analysis)

資料分析探索 (Explorator Data Analysis) 是讓我們對收集到的資料有充分的了解。包含了
房價分佈 : 每個房價的分佈圖
相關特徵 : 那些事情 (特徵) 對房價的影響特別力害，
無關特徵 : 那些事情 (特徵) 對房價沒啥影響。

房價分佈

底下使用 sns顯示 df[‘PRICE’] ，也就是顯示每一間房屋的價格分佈

import seaborn as sns
import pylab as plt
sns.set_style('whitegrid')
sns.histplot(df['PRICE'], kde=True)
plt.show()

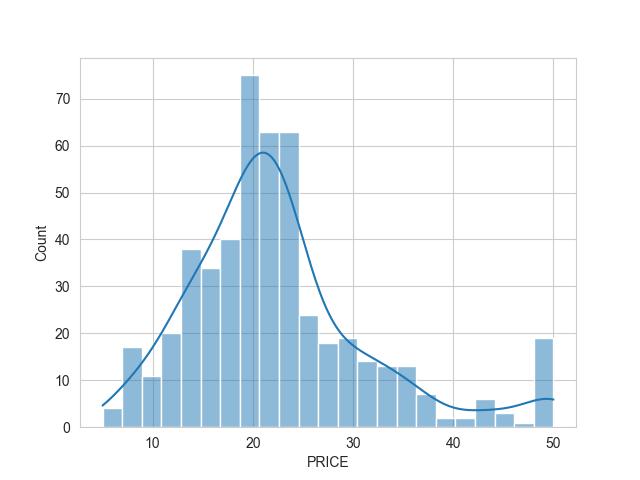
上述的海生圖，有點偏向左邊，右邊的豪宅比較稀疏，這就會影響我們預測的準度。

為什麼會影響呢? 試想一下，郭台銘一個人拉高了多少我們的國民平均所得。這種貧富愈不均的情形下，預測就會愈不準確。所以後續章節會討論如何把最高值往右拉到整個圖的中心。

皮爾森積差-Pearson

皮爾森積差(perason) 是將每個特徵與其它特徵進行計算，計算後的值介於 -1~1之間。0 表示沒有任何相關性，接近 -1 或 1 則表示相關性非強常。

皮爾森積差的公式為 $(r=\frac{\sum_{i=1}^{n}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum_{i=1}^{n}(X_i-\overline{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i-\overline{Y})^2}})$

二個變數量 X , Y。 $(\overline{X})$為 X 的平均數， $(\overline{Y})$為 Y 的平均數。

$(\sum_{i=1}^{n}(X_i-\overline{X})(Y_i-\overline{Y}))$ 稱為共變異數，又稱為協方差(Convariance)

$(\sqrt{\sum_{i=1}^{n}(X_i-\overline{X})^2})$ 為 X 的標準差(standard deviation)。

協方差 / (X 標準差 * Y 標準差)，就是皮爾森積差。

底下代碼手動使用Python代碼計算皮爾森積差

import numpy as np
np.random.seed(1)
#x', y'為x, y的平均數
#(x0-x')(y0-y')+(x1-x')(y1-y')+(x2-x')(y2-y')+...+(xn-x')(yn-y')
x=np.random.randint(1, 100, 10)
y=np.random.randint(1, 100, 10)
xmean=x.mean()
ymean=y.mean()
print("x:",x)
print("y:",y)
print("x_mean:",xmean)
print("y_mean:",ymean)
#共異變數/斜方差Convariance =>(38-38)*(77-39.9)+(13-38)*(72-39.9)+.....+(2-38)*(29-39.9))
convariance=np.sum((x-xmean)*(y-ymean))
print(f'斜方差 : {convariance}')
xd=np.sqrt(np.square(x-xmean).sum())
yd=np.sqrt(np.square(y-ymean).sum())
#皮爾森積差其值一定會介於 -1~1之間
p=convariance/(xd*yd)
print(f"皮爾森積差 : {p}")
import pandas as pd
df=pd.DataFrame(data={"x":x, "y":y})
print(f'df自動計算皮爾森積差 : \n{df.corr()}')
結果 : 
x: [38 13 73 10 76  6 80 65 17  2]
y: [77 72  7 26 51 21 19 85 12 29]
x_mean: 38.0
y_mean: 39.9
斜方差 : 779.9999999999998
皮爾森積差 : 0.09304301976479494
df自動計算皮爾森積差 : 
          x         y
x  1.000000  0.093043
y  0.093043  1.000000

為什麼皮爾森積差接近 -1 及 1 時相關性非常強呢? 這個是很深的數學原理，有興趣的人可上網 google一下。

因為皮爾森積差常被拿來運用，每次都要寫上述的程式非常麻煩。所以 DataFrame 開發了 corr 方法計算皮爾遜積差。但皮爾森系數只是一堆數字，人類是無法理解的，所以總是使用熱度圖來視覺化皮爾森積差。

from sklearn.datasets import load_boston
import seaborn as sns
import pylab as plt
import pandas as pd

boston_dataset = load_boston()
print(boston_dataset.data.shape)
df=pd.DataFrame(data=boston_dataset.data, columns=boston_dataset.feature_names)
df.insert(0, column="PRICE", value=boston_dataset.target)
corrmat=df.corr()
sns.set(font_scale=0.7)
sns.heatmap(corrmat, annot=True, annot_kws={'size':6}, fmt='.2f')
plt.savefig("boston_3.jpg")
plt.show()

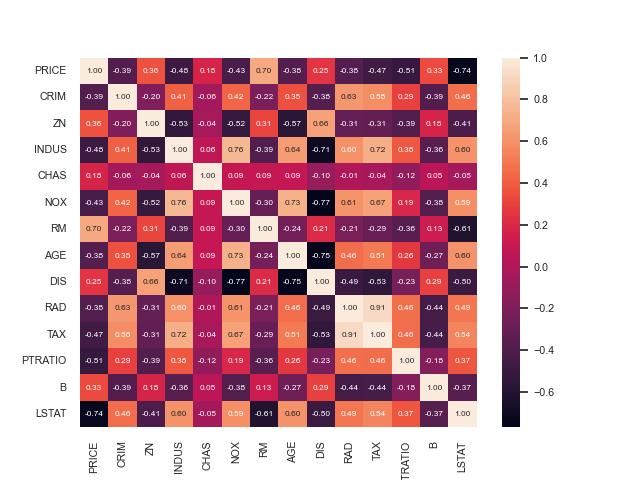
上圖，可以看出PRICE(售價)與RM(房子的房間數)及LSTAT(中低收入戶在此處的人口比例)有著極強的關係。中間的對角線是自已本身跟自已的內差，所以一定是1。

為了更清楚表示，使用 corrmat.nlargest()對 ‘PRICE’ 欄位由大到小進行排序

import seaborn as sns
import pylab as plt
corrmat=df.corr()
corrmat=corrmat.nlargest(len(corrmat), columns='PRICE')
sns.set(font_scale=0.7)
sns.heatmap(corrmat, annot=True, annot_kws={'size':6}, fmt='.2f')
plt.savefig("boston_4.jpg")
plt.show()

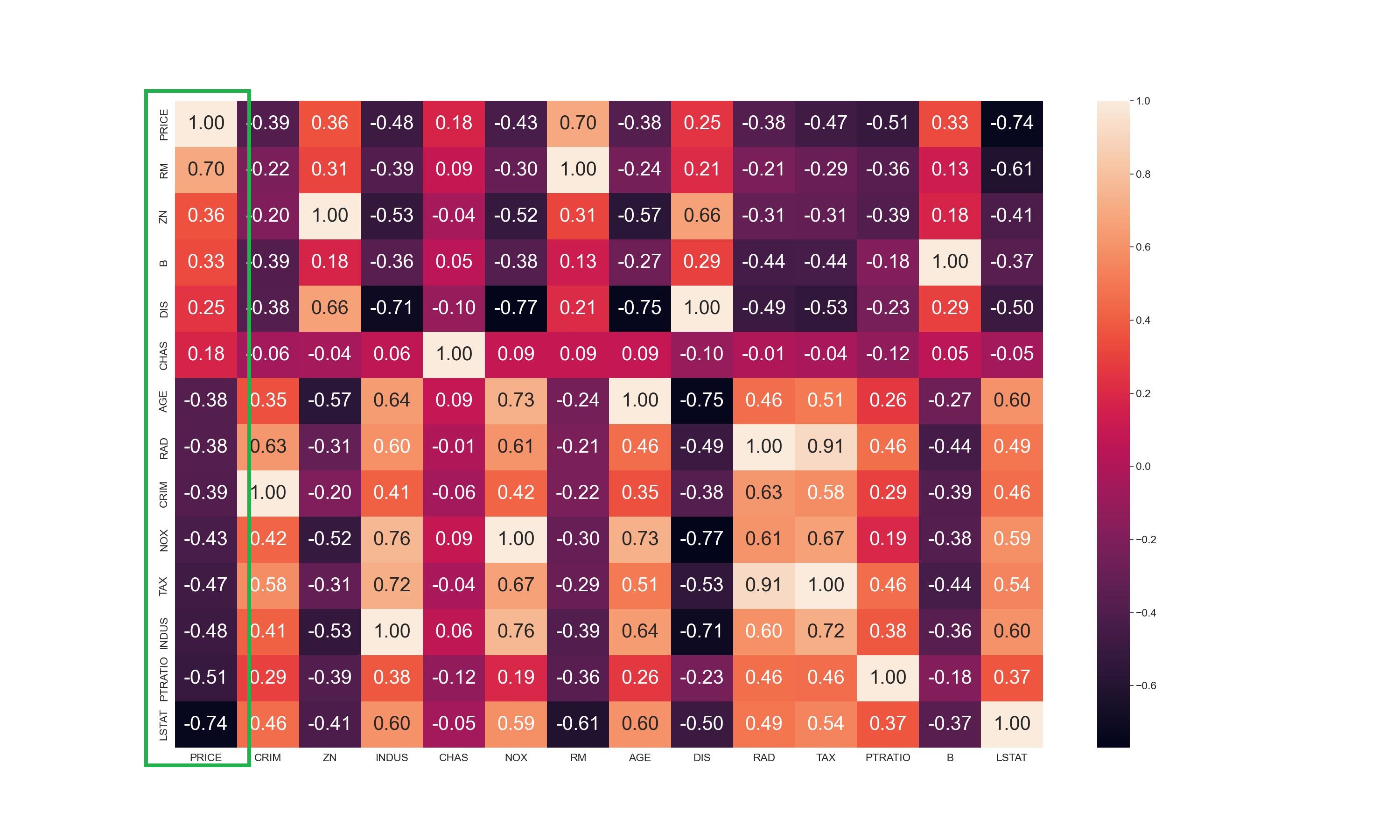
一經排序，當然對角線就不是1.0了。

房價與RM/LSTAT關係圖

底下代碼可以看到房價跟 LSTAT (中低收入戶佔當地居住人口的比例) 呈現反向的線性關係，而房價與RM (每間房子的房間數) 呈現正向的線性關係。

import pylab as plt
features=['LSTAT','RM']
plt.figure(figsize=(20,5))
for i, col in enumerate(features):
    plt.subplot(1, len(features), i+1)
    x=df[col]
    y=df['PRICE']
    plt.scatter(x, y)
    plt.title(col)
    plt.xlabel(col)
    plt.ylabel('PRICE')
plt.show()

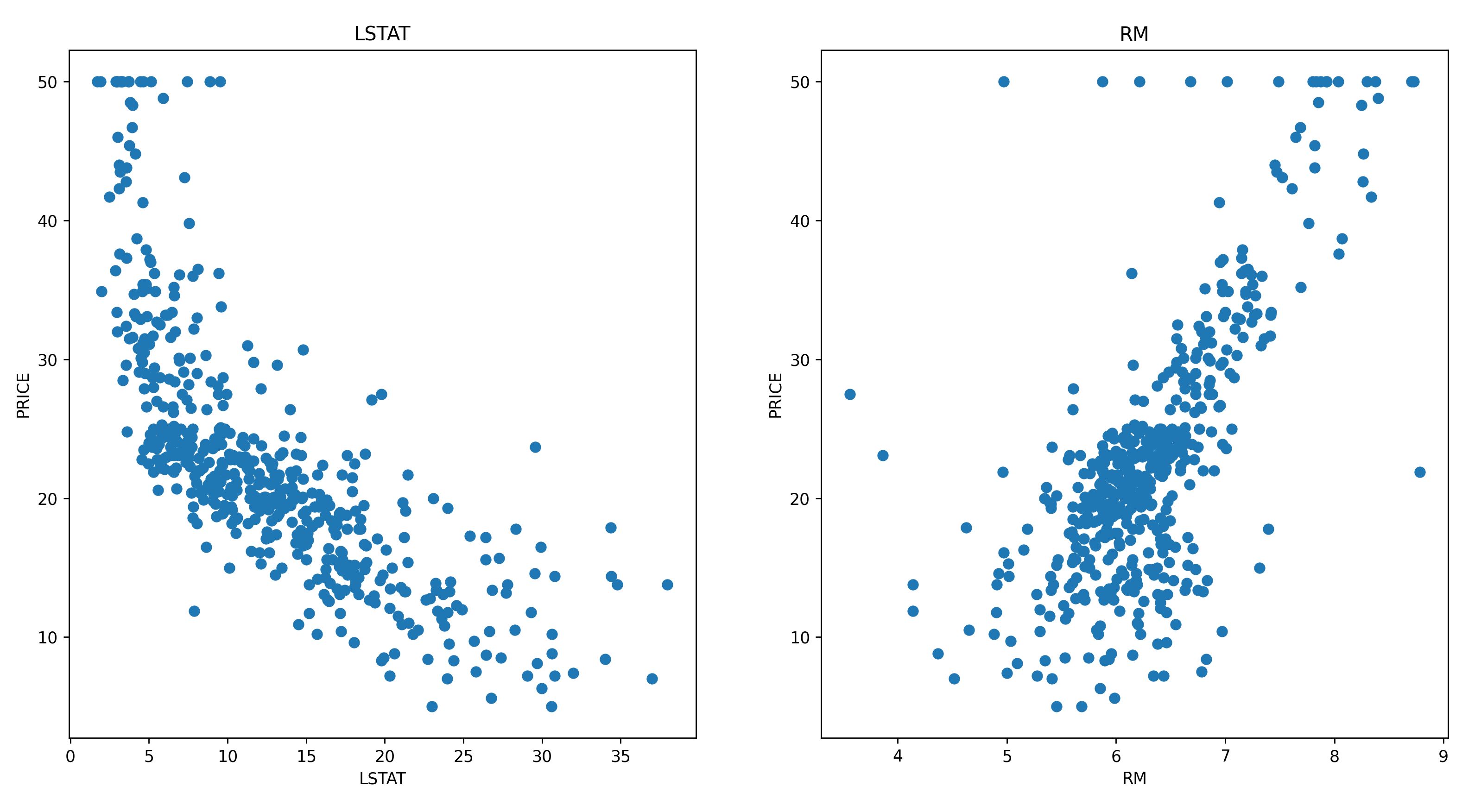
特徵工程

在EDA之後，還需進行特徵工程，填入空值，並將離群值刪除。本例尚不需這麼麻煩，所以跳過。

詳細說明請參考本人撰寫的 Skewness 說明

建立訓練模型

先將 LSTAT 及 RM 合併成x 軸的二個特徵，y軸為房價，再使用 train_test_split 將資料分成 80%的訓練資料及 20% 的測試資料。

LSTAT 及 RM 合併使用 np.c_[] 欄合併，np.c_的用法如下

import numpy as np
a=[1,2,3,4]
b=[5,6,7,8]
c=np.c_[a,b]
print(c)
結果:
[[1 5]
 [2 6]
 [3 7]
 [4 8]]

最後建立線性回歸模型，開始訓練。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
data=np.c_[df['LSTAT'], df['RM']]
x=pd.DataFrame(data=data, columns=['LSTAT','RM'])
y=df['PRICE']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state=5)
model=LinearRegression()
#開始訓練
model.fit(x_train, y_train)

預測

底下的 model.score，會使用 x_test的測試資料進行預測房價，然後再跟實際的 y_test房價進行評分。分數若能達到 1.0 當然是最準確，此例可以達到 0.66289 已經是非常的高了。

若只需預測，只需使用 model.predict即可。底下將實際房價 y_test 與預測值 y_pred zip在一起，方便觀查之間的差異。

#底下的model.score, 會使用 x_test的資料進行預測房價,
#再將預測的房價與實際的 y_test房價進行評分
print(f'score:{model.score(x_test, y_test)}')#0.6628996975186952

#底下僅進行預測，將預測與實際合併再一起進行觀測
y_pred=model.predict(x_test)
for i in zip(y_pred, y_test):
    print(i)
結果:
score:0.6628996975186952
(37.38999403450201, 37.6)
(29.79290610929409, 27.9)
(25.86755297466814, 22.6)
(0.31370828082136093, 13.8)
(33.313855585417315, 35.2)

模型訓練及儲存.py

底下是讀取資料，建模，訓練的完整代碼

from sklearn.datasets import load_boston
import pandas as pd
display=pd.options.display
display.max_columns=None
display.max_rows=None
display.width=None
display.max_colwidth=None
boston_dataset = load_boston()
df=pd.DataFrame(data=boston_dataset.data, columns=boston_dataset.feature_names)
df.insert(0, column="PRICE", value=boston_dataset.target)
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
data=np.c_[df['LSTAT'], df['RM']]
x=pd.DataFrame(data=data, columns=['LSTAT','RM'])
y=df['PRICE']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state=5)
model=LinearRegression()
#開始訓練
model.fit(x_train, y_train)

pickle.dump(model, open("house.model", "wb"))

模型載入及預測.py

底下是載入模型，預測的完整代碼

import pickle
from sklearn.datasets import load_boston
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

datas=load_boston()
df=pd.DataFrame(data=datas.data, columns=datas.feature_names)
df.insert(0, column='PRICE', value=datas.target)
data=np.c_[df['LSTAT'],df['RM']]
x=pd.DataFrame(data=data, columns=['LSTA','RM'])
y=df['PRICE']
x_train, x_test, y_train, y_test=train_test_split(x,y, test_size=0.2, random_state=5)

#模型載入及預測
model=pickle.load(open("house.model",'rb'))
score=model.score(x_test, y_test)
print(score)#不是精準度，而是信心度
#predict : 開始預測
pre_price=model.predict(x_test)
for i in zip(pre_price, y_test):
    print(i)