本章節出現在數學篇是為了講解微分的方法。
但在AI TensorFlow章節又重新列出，是為了講解梯次下降的方法。

二都關係密切，所以必需完全了解。

一元二次方程式求解

$(ax^{2}+bx+c=0)$

二邊除a : $(x^{2}+\frac{bx}{a}+\frac{c}{a}=0)$

$(\therefore x^{2}+\frac{bx}{a}=-\frac{c}{a})$

二邊加上$((\frac{b}{2a})^{2})$  => $(x^{2}+\frac{bx}{a}+(\frac{b}{2a})^{2}=-\frac{c}{a}+(\frac{b}{2a})^{2})$

$(\therefore (x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}})$

$(x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a})$

導數

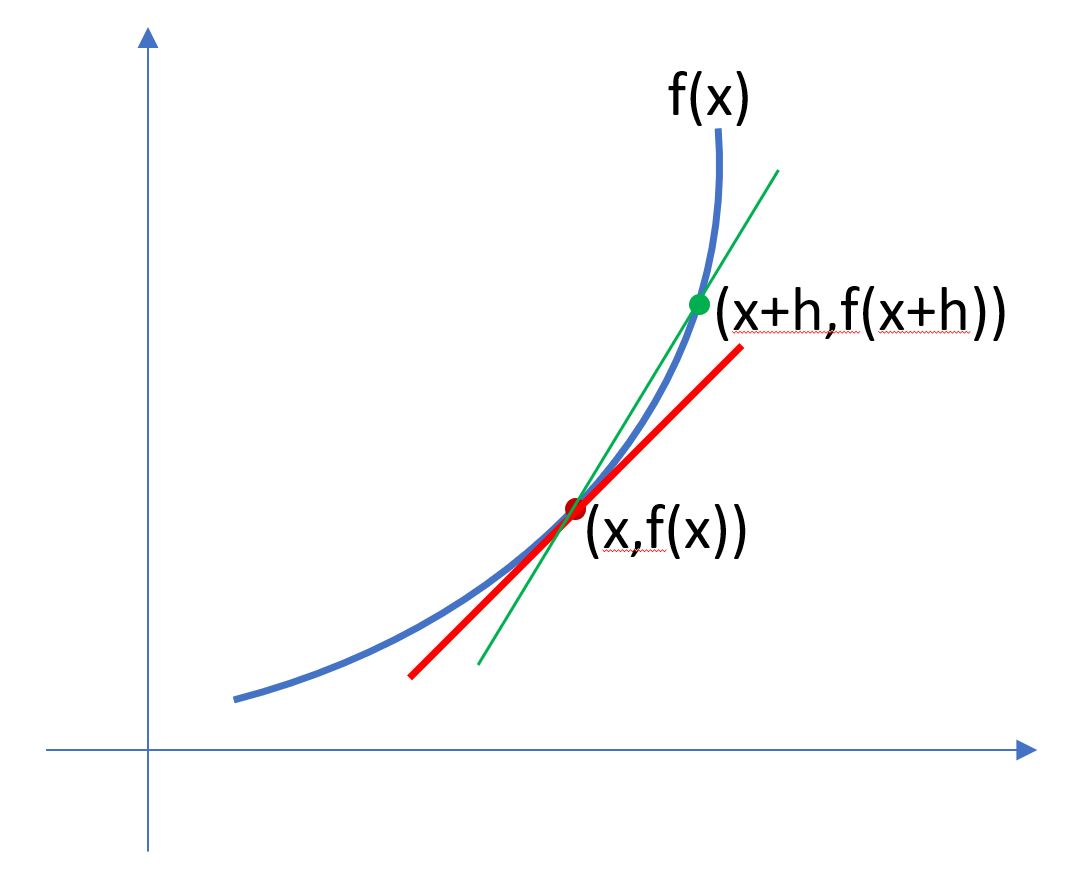
上圖藍色曲線的方程式，假設為 f(x)，則(x, f(x))這個點的切線(紅色線)斜線為多少呢?。

首先x往右邊增加一個h的值，其y軸為f(x+h)，所以綠色(割線)斜率為$(\frac{f(x+h)-f(x)}{h})$

當h往左邊靠，一直逼近x時，那就是紅色線的斜率 $(\lim_{h\to0}\frac{f(x+h)-f(x)}{h})$

把上面的那個式子，給予一個變數 $(f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h})$, 則$(f'(x))$稱為導數
所以導數就是某個點的斜率。

假設$(f(x)=x^{2})$，則斜率為

$(\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^{2}-x^{2}}{h}=\frac{x^{2}+2xh+h^{2}-x^{2}}{h}=2x+h)$

$(f'(x)=\lim_{h\to0}2x+h = 2x)$

也就是說，x=1時，斜率為2, x=2時，斜率為4

而$(f'(x)=2x)$ 正是 $(x^{2})$的微分，也就是說，導數就是切線，也就是微分後的函數

偏微分

上述的方程式，只有一元變數(x)。如果是多元呢，如下所示

$(f(x_{1},x_{2})=ax+1=\begin{bmatrix}10&1\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}+1=10x_{1}+x_{2}+1)$

$(\bigtriangledown f(x_{1},x_{2})=\begin{bmatrix}\frac{\partial f(x)}{\partial x_{1}} \\ \frac{\partial f(x)}{\partial x_{2}}\end{bmatrix}=\begin{bmatrix}
\frac{\partial(10x_{1}+x_{2}+1))}{\partial x_{1}}
\\
\frac{\partial(10x_{1}+x_{2}+1))}{\partial x_{2}}
\end{bmatrix}
=\begin{bmatrix}
10
\\
1
\end{bmatrix})$

多次多元方程式偏微分

$(f(x_{1}, x_{2})=5x_{1}^{2}+2x_{2}^{2}+7x_{1}x_{2}+10x_{1}+x_{2}+1)$

偏微分後為 $(f'(x_{1}, x_{2})=\begin{bmatrix}
10x_{1}+7x_{2}+10
\\
4x_{2}+7x_{1}+1
\end{bmatrix})$

由上可推出，如果是2元方程式，就是2*1矩陣，如果是 3元方程式，就是3*1矩陣

梯度下降

梯度下降(Gradient Descent)，目的是在使用逼近法尋找最接近的函數

import numpy as np
import pylab as plt
px=[1,0, -1]
py=[1, 0, -3]

reg=np.poly1d(np.polyfit(px, py, 1))
plt.plot(px, reg(px), color='green')

x=np.linspace(-1.5, 1.5, 2)
y=3*x+1
plt.plot(x, y, color='red')

plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei']
plt.rcParams['axes.unicode_minus'] = False
plt.legend(['迴歸', '假設'] )
plt.scatter(px, py)
plt.plot([-4, 4], [0, 0], color='blue')
plt.plot([0, 0], [-4, 4], color='blue')
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.grid(True)
plt.show()

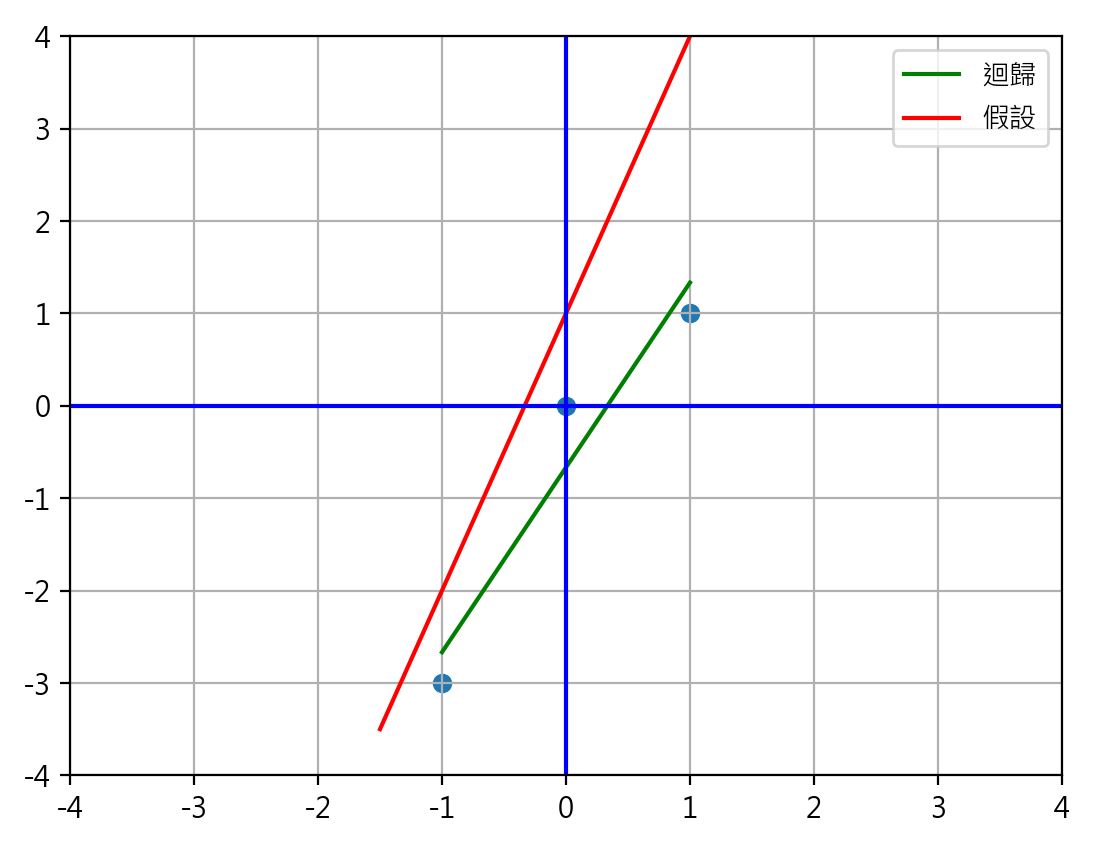
如上圖，假設有三個點(目標點)分別為(1, 1), (0, 0), (-1, -3)。如果我們要找一條線最接近這三個點。依以前的想法，那就是綠色那條迴歸線了。但迴歸線又是怎麼找出來的呢?
在此我們先隨便假設一條線，如紅色的 f1(x)=3x+1 這個函數。然後把三個點的x值代入f1函數，得到的y值如下

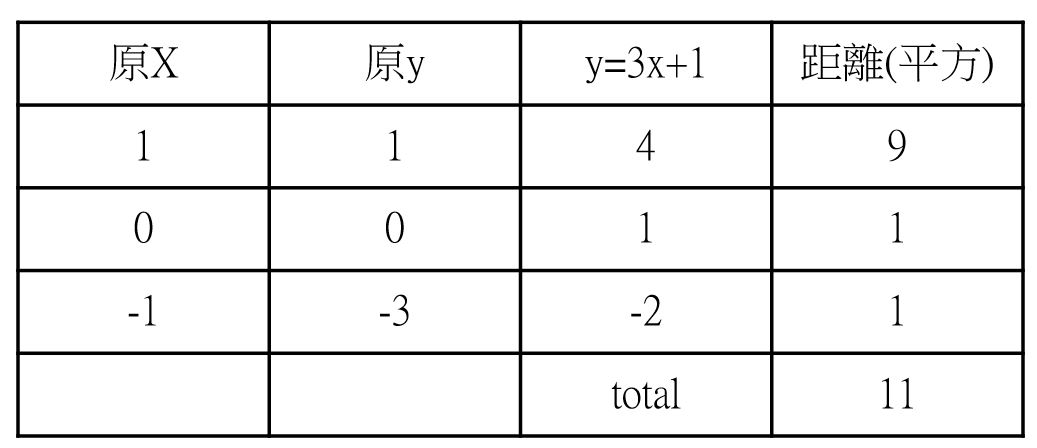
上述3x+1所求出的y值，與目標點的y值相減後的平方，加總為11。為什麼要平方呢? 這樣才不會有負值出現. 即總距離為
$(\sum_{i=0}^{i=n}(y_{ni}-y_{oi})^{2})$ 
$(y_{ni})$ 為目標點的y值，$(y_{oi})$ 為目標點的y值

這樣可以解釋迴歸線跟PCA的差異了吧。PCA是三點的投影距離總和的最小值。迴歸線是三點的y值與原點最小總值。

再以上例$(f(x)=x^{2}-10x+1)$為例，x為多少時，有最小極值呢。用上述的一階微階可知 $(f'(x)=2x-10)$，當x=5時，表示斜率為0，有極值，所以f(5)=-24。但較複雜的函數並不是都可以使用此方法求值。此時就要用逼進法(梯度下降)。

再以上述$(x^{(t+1)}=x^{t}-\gamma f'(x^{(t)})=x^{t}-\gamma (2x^{(t)}-10)=(1-2\gamma )x^{(t)}+10\gamma )$
$(\gamma )$ : 學習函數，每次要進步的值
$(x^{{t}})$ : 當下x的值
$(x^{{t+1}})$ : 下一次x的逼進值

$(\gamma )$ 的值複雜亦常，太大也不行，太小也不行，這又有一套理論，所以可以先跳過

損失函數

再以$(f(x)=x^{2}-10x+1)$為例
$(L=\sum (y-(x^{2}-10x+1))^2)$, 即 (目標點y-新點y)的平方總和。

加速度

距離與加速度的公式為 : $(S=v_{0}t+\frac{1}{2}at^{2})$

對t 進行一次微分後，就是某個時間點的瞬間速度了

$(v=v_{0}+at)$

todo : 損失函數 https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E6%B7%B1%E5%BA%A6%E5%AD%B8%E7%BF%92-%E5%9F%BA%E7%A4%8E%E4%BB%8B%E7%B4%B9-%E6%90%8D%E5%A4%B1%E5%87%BD%E6%95%B8-loss-function-2dcac5ebb6cb