向量Vector

向量是方向的量化，或方向數位化的簡稱。描述方向的方式，可以用右上30度，左下45度。

這種描述的方式，對人類而言很直覺，但在數學或電腦上，無法計算。所以就量化成 x, y二軸的數字(3, 4)

todo

下圖紅色線 z 是由 x 及 y 二條綠色線組成。所以我們定義 $(\vec{z}=\vec{x}+\vec{y})$

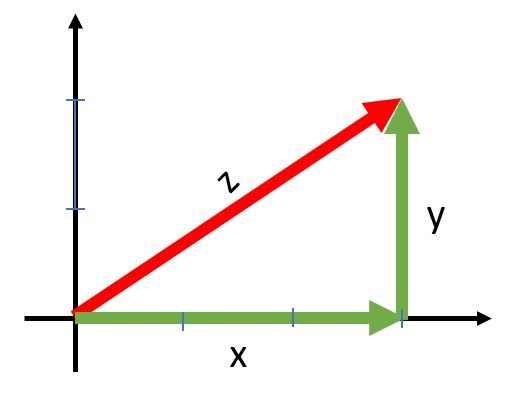
對於向量的寫法，總是有點難懂。把它想像成是一艘太空船，以水平3km/hr的速度往右，垂直2km/hr的速度往上。所以這艘太空船就會以$(\sqrt{3*3+2*2}=\sqrt{13})$的速度往$(\vec{z})$的方向前進。

基底向量

我們定義$(\vec{i}=\begin{bmatrix}1\\0\end{bmatrix} , \vec{j}=\begin{bmatrix}0\\1\end{bmatrix})$

上述的$(\vec{x})$及$(\vec{y})$分別為

$(\vec{x}=3 * \begin{bmatrix}1\\0\end{bmatrix})$

$(\vec{y}=2 * \begin{bmatrix}0\\1\end{bmatrix})$

所以$(\vec{z}=\vec{x}+\vec{y}=3*\vec{i}+2*\vec{j})$

$(\vec{i})$及$(\vec{j})$，我們稱為基底向量。以1為主的基底向量，稱為標準基底向量。此時有二個變數 3, 2，亦稱為二個特徵。

變更基底向量

如果上述的基底向量變更為
$(\vec{v}=\begin{bmatrix}1.5\\1\end{bmatrix})$，此時$(\vec{z}=2*\vec{v})$
若再變成
$(\vec{v}=\begin{bmatrix}3\\2\end{bmatrix})$，此時$(\vec{z}=1*\vec{v})$

也就是整個圖轉成如下的樣子，此時只需一個變數 “2” 或 “1” 即可描述整個向量。此時特徵就會變成只有一個

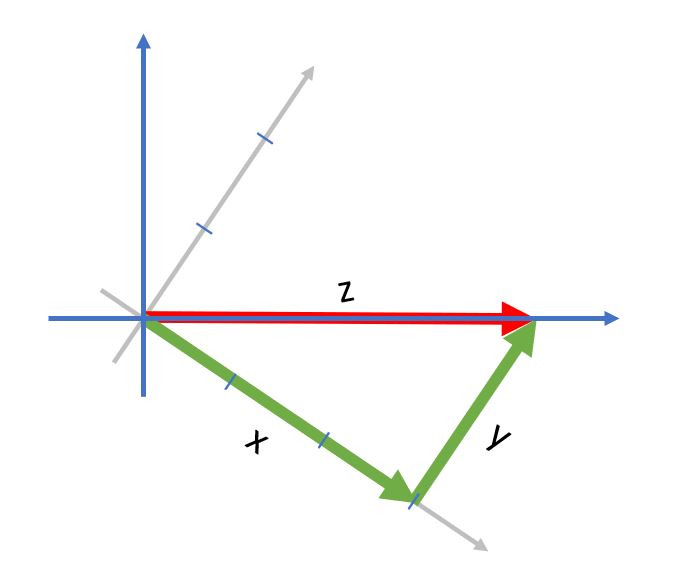
說的更直白一點，$(\vec{v})$就是我們要巔覆傳統的度量衡單位，創造另一個新的單位。比如現今有一公尺，一公里。但我們就是要創造一個新的單位，比如~~一光秒(光一秒跑的距離)。那麼太陽離地球的距離就不再是1.5億(150,000,000)公里，而是500光秒，也就是8.3光分，如此簡化了很多個 “0”。

向量就是 2*1矩陣

上述不論是$(\vec{v}=\begin{bmatrix}3\\2\end{bmatrix})$ 或是 $(\vec{i}= \begin{bmatrix}1\\0\end{bmatrix})$
可以很明顯的看出，原來向量就是一個 2*1的矩陣$(\begin{bmatrix}
x\\y\end{bmatrix})$，也就是$(\begin{bmatrix}x,y \end{bmatrix}^{T})$

張量(Tensor)

以圖片像素為例，每個像素皆有(r, g, b)三個值。我們稱每個點的(r, g, b) 為一個向量。而如下黃色區域每一個格點都有一個向量。這些眾多向量的集合，稱為張量。也就是說，張量是由多個向量組成。

說的更貼切一點，就是在二維平面上，每個點又有多個特徵的意思。拓展開來，m個維度上，每個點又有n個特徵