熟記

interp1d(x, y):產生線性插值方程式
interp1d(x, y, kind='cubic'):取得三次插值法函數

繪製圓點

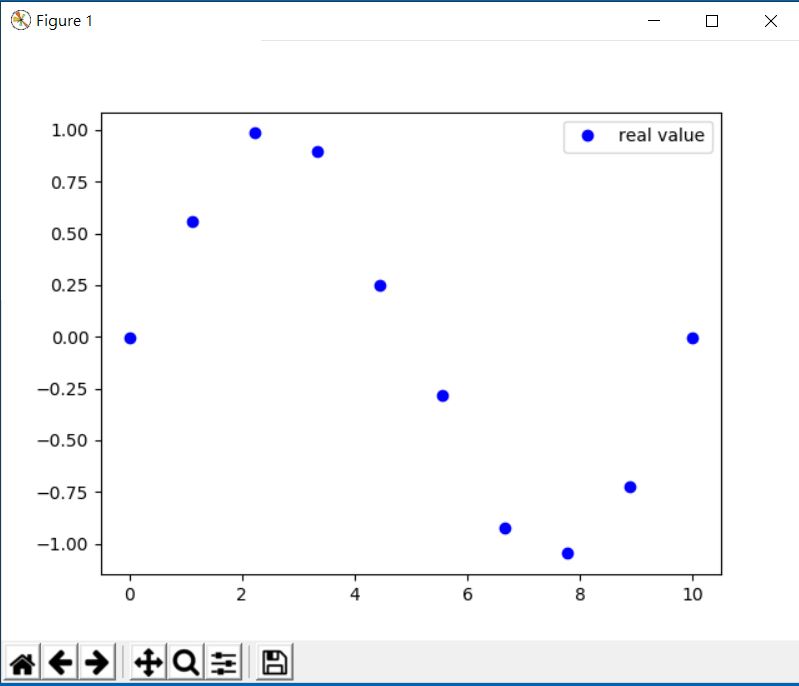
底下的代碼, 先產生0~10之間10個數, 再用sin產生正弦波10個點, 然後使用亂數加入雜訊噪音, 最後將這10個點繪製在圖表上.

plt.plot()第一參數為x軸, 第二參數為y軸的值, 第三參數”bo” 解說如下
第一字元 : b 藍色, g 綠色, r 紅色, y黃色
第二字元 : o 圓點, s 方塊, ^ 三角型

import numpy as np
import pylab as plt

time = np.linspace(0, 10, 10)
noise = (np.random.random(10)*2 - 1) * 0.1
value = np.sin(2 * np.pi * time) + noise
plt.plot(time, value, 'b^', ms=6, label='real value')

線性插值(Interpolate [ɪnˋtɝpə͵let])

當我們在表現資料時，常常會有需要比實際量測點上的值更細密的情況，或者是有需要在範圍外預測其值。比方說天氣圖的繪製，不論是氣壓或是雨量，都不可能做到處處都有測量站，又例如我們關心一天之中溫度隨時間的變化，但是實際上記錄氣溫的動作可能只是每小時一次，則我們要作一個連續的圖時，就會用到插值法。

數學的數值分析領域中，內插或稱插值(interpolation)是一種通過已知的、離散的數據點，在範圍內推求新數據點的方法. 通過採樣或實驗取得的數據點是有限的. 若希望在有限的數據中獲得一個連續的函數(也就是曲線), 則可使用插值法. 插值法當然會有誤差, 但其效能遠大於精度的損失. 

繼上面的代碼, 再加入如下, 即可繪制更細的點或線

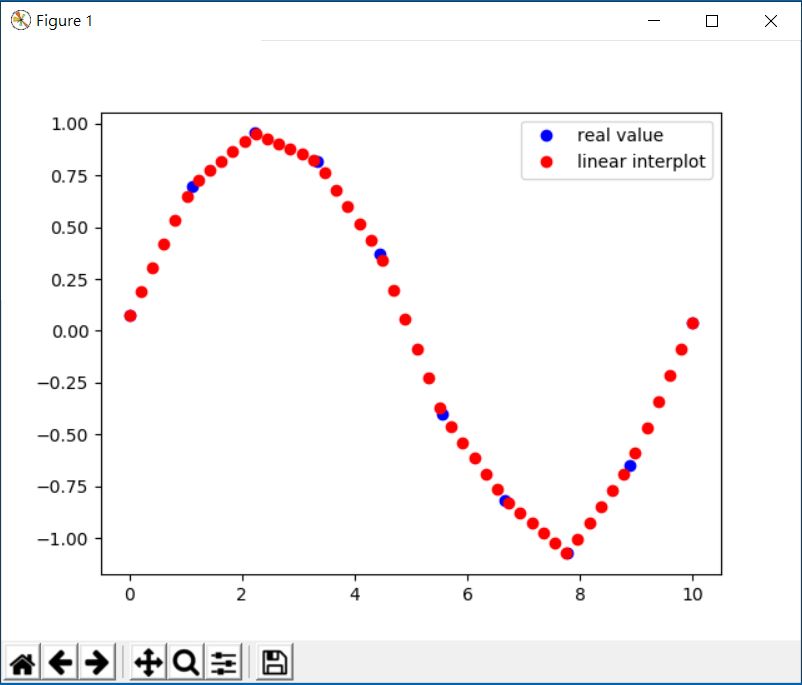
from scipy.interpolate import interp1d # 注意喔, 是數字的 1
f1 = interp1d(time, value) #產生線性插值函數
x = np.linspace(0, 10, 50)#將間隔細分為50個區段
y = f1(x)#利用線性插值函數產生50個插值
plt.plot(x, y, "ro", label='linear interplot')

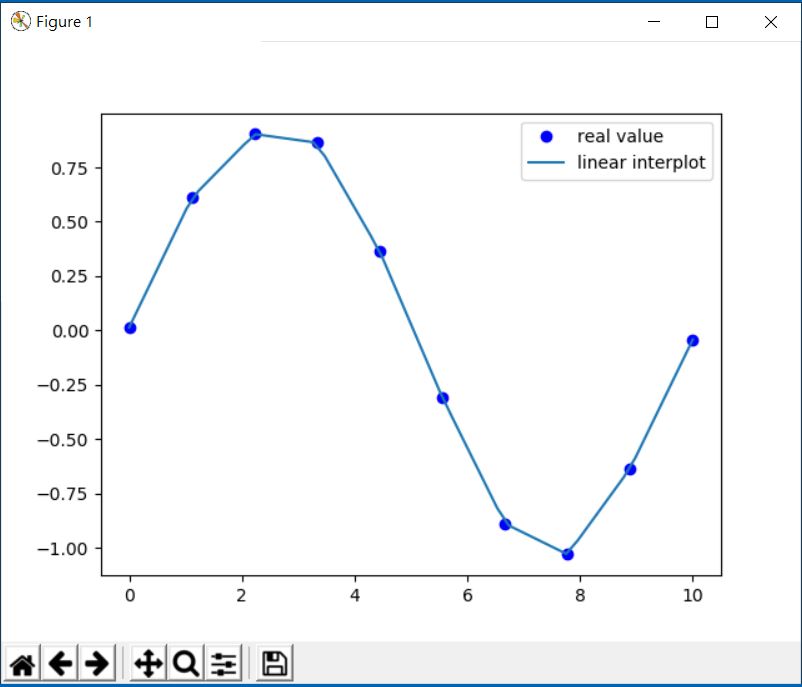
f1 = interp1d(time, value) #產生線性插值函數
x = np.linspace(0, 10, 50)#將間隔細分為50個區段
y = linear_interp(x)#利用線性插值函數產生50個插值
plt.plot(x, y, label='linear interplot')

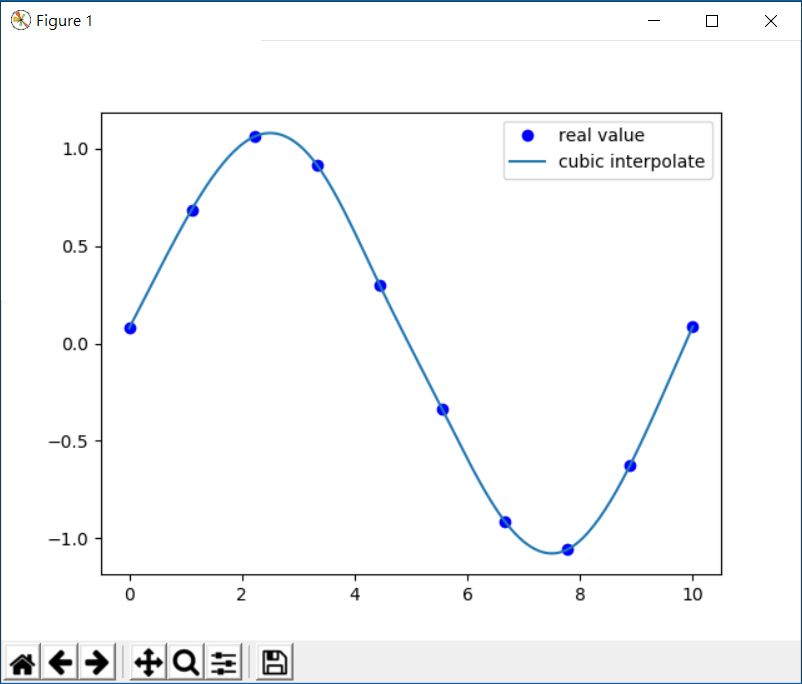
多項式插值法

三次插值法(cubic interpolation method)又稱多項式插值法, 逐次以三次曲線φ(t)=a₀+a₁t+a₂t²+a₃t³極小點逼近尋求函數f(t)極小點的一種方法.具體做法是：假設t₁<t₂ 在搜索區間[t₁，t₂]中以φ(t)擬合f(t), 使滿足φ(t_i)=f(t_i),φ'(t_i)=f'(t_i), (i=1,2)（此式記為(1)式）對φ(t)求導並令其等於零, 求得φ(t)在[t₁，t₂]中由a₀，a₁，a₂和a₃表示的極小點運算式, 再由方程組(1)解得a₀，a₁，a₂和a₃，將其代入此運算式, 便得f(t)的近似極小點, 逐次反覆運算, 當φ(t)在近似極小點處的導數值的絕對值小於某給定誤差時, 反覆運算停止. 三次插值法尋求極小點比二次插值法(抛物線插值法)有更快的收斂速度, 但其每一輪反覆運算的計算量則比二次插值法要大.

請將下面代碼加入, 即可獲得平滑的曲線

x=np.linspace(0, 10, 200)
f3 = interp1d(time, value, kind='cubic')#取得三次插值法函數
y = f3(x)#取得三次插值的值
plt.plot(x, y, label='cubic interpolate')