m/s 轉 km/hr

每秒 m 公尺，轉成每小時 x 公里的公式為 
x =m *3600/1000 = m *3.6

卡迪兒座標系(Cartesian coordinate system)

我們常稱的xy座標，或是xyz立体空間座標，就是卡迪兒座標系，這傢伙是法國人。由二個或三個正交線所組成的。如下圖為3D立体座標系。

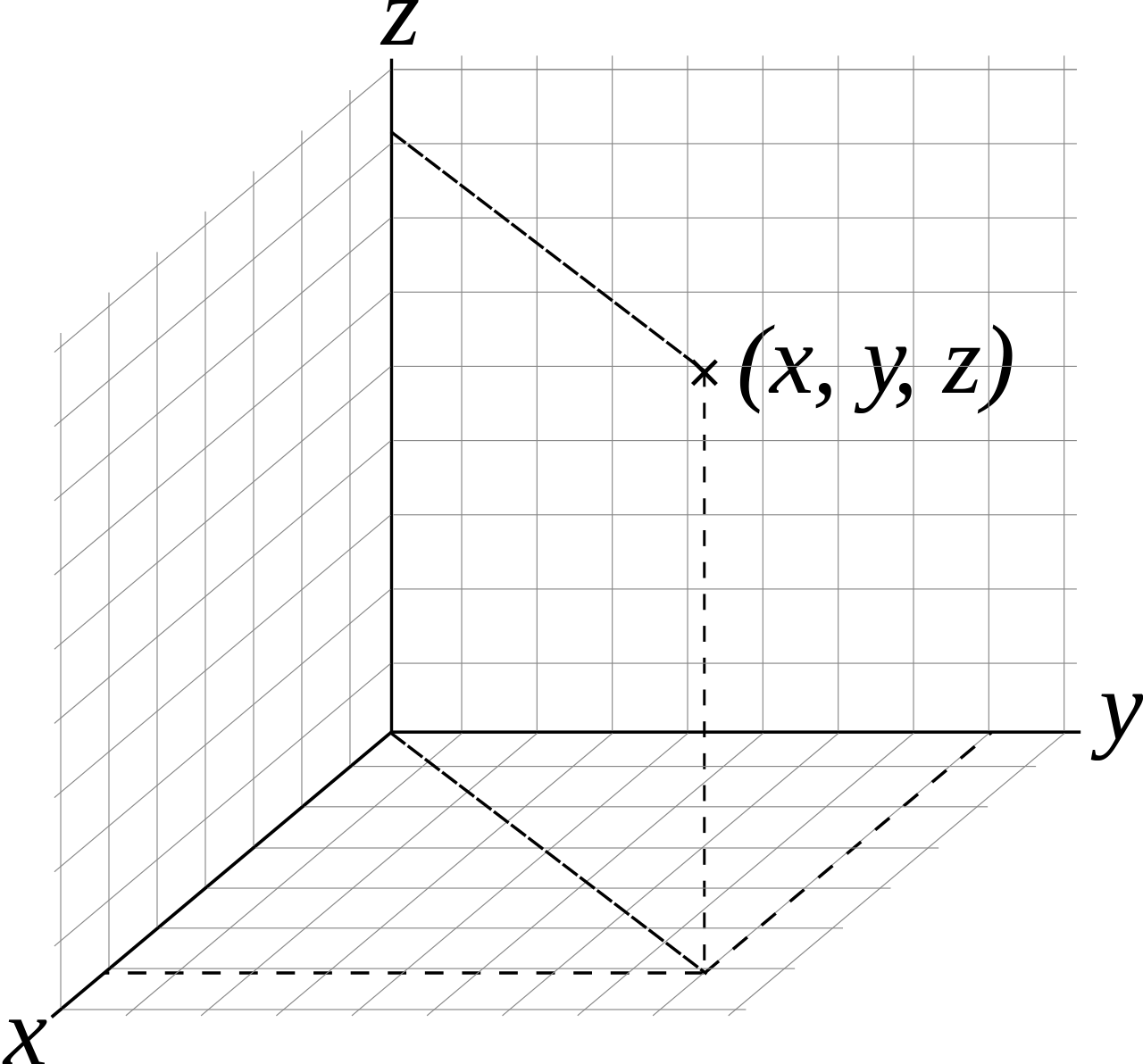
三角函數

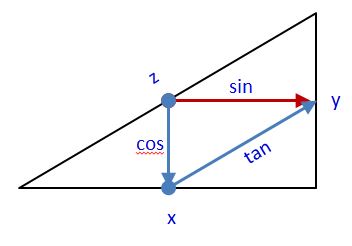
$sin\theta =\frac{y}{z}$

$cos\theta =\frac{x}{z}$

$tan\theta =\frac{y}{x}$

三角面積 : $\frac{x*y}{2}$

反三角函數 : $sin^{-1}(\frac{y}{z})$=角度

弧度(弳度) : $1^{o}=\frac{\pi}{180}$

圓公式

圓周 : $2\pi r$
圓面積 : $\pi r^{2}$
正弦波 : $f(x)=A*sin(k\pi t)$ : A為振幅，k 為波峰數，t 為時間

圓函數

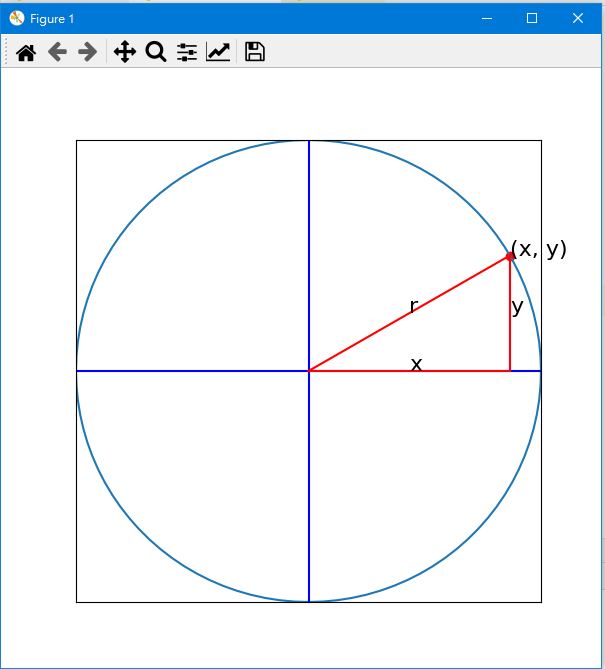
上述的圖形，由下面的Python代碼所繪製而成的。(x, y)座標點中，x, y分別為

$x=r*cos(\frac{\pi}{180}*\theta)$
$y=r*sin(\frac{\pi}{180}*\theta)$

當$\theta$ 由 0變換到360度時，即形成一個圓

import numpy as np
import pylab as plt
r=10
n=100
x=[]
y=[]
for i in range(n+1):
    angle=360/n*i
    x.append(r*np.cos(np.pi/180*angle))
    y.append(r * np.sin(np.pi / 180 * angle))
plt.figure(figsize=(6,6))
plt.xticks([])
plt.yticks([])
plt.plot(x, y)
plt.xlim(-r, r)
plt.ylim(-r, r)
plt.plot([-r, r],[0, 0], color='blue')#畫X軸
plt.plot([0, 0],[-r, r], color='blue')#畫y軸
#底下畫個三角型
x1=r*np.cos(np.pi/180*30)
y1=r*np.sin(np.pi/180*30)
plt.scatter([x1],[y1], color='red')#畫點
plt.text(x1, y1,s='(x, y)', fontsize=16)
plt.text(x1/2,0 ,s='x', fontsize=16)
plt.text(x1, y1/2 ,s='y', fontsize=16)
plt.text(x1/2, y1/2 ,s='r', fontsize=16)
plt.plot([x1, x1],[0, y1], color='red')
plt.plot([0, x1],[0, y1], color='red')
plt.plot([0, x1],[0, 0], color='red')

plt.show()

一元二次方程式求解

$ax^{2}+bx+c=0$

二邊除a : $x^{2}+\frac{bx}{a}+\frac{c}{a}=0$

$\therefore x^{2}+\frac{bx}{a}=-\frac{c}{a}$

二邊加上$(\frac{b}{2a})^{2}$  => $x^{2}+\frac{bx}{a}+(\frac{b}{2a})^{2}=-\frac{c}{a}+(\frac{b}{2a})^{2}$

$\therefore (x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}}$

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

總和公式

$\sum_{i=1}^{i=n}x_{i}=x_{1}+x_{2}+…+x_{n}$

平均數(Mean)

$\mu =\frac{1}{n}\sum_{i=1}^{i=n}x_{i}=\frac{x_{1}+x_{2}+…+x_{n}}{n}$

$\sum$ 唸成 Sigma

sum=0
import numpy as np
rng=np.random.RandomState(0) #偽亂數
d=rng.randint(1,100,10)
print(d)

sum=0
for i in d:
    sum+=i
print('用迴圈計算總合 : ', sum, '<==速度很慢')
print('d.sum() : ', d.sum(), '<==調用C語言執行，速度超極快')
u=d.mean()
print('sum/10 = ', sum/10)
print('d.mean() ', d.mean(), '<==調用C語言執行，速度超極快')

結果 : 
[45 48 65 68 68 10 84 22 37 88]
用迴圈計算總合 : 535 <==速度很慢
d.sum() : 535 <==調用C語言執行，速度超極快
sum/10 = 53.5
d.mean() 53.5 <==調用C語言執行，速度超極快

用迴圈計算總和，是傳統語言必會的技術。但在Python使用迴圈則效能太差。需使用d.sum()調用C語言來執行，速度才會快. 

變異數(Variance)

何謂變異數?? 假設有二個國家，每個國家有5個人
美國 : 五個人分別收入為 [10000,100000,5000,5000,5000]
台灣 : 五個人分別收入為[30000,30000,30000,30000,30000]

經計算 :
美國 : 變異數 : 1,410,000,000, 標準差 : 37,549.96
台灣 : 變異數 : 0，標準差 : 0
由上的數字，可以得知美國的貧富差異實在是大的不得了。因為就可以用這組數字來描述貧富差異的嚴重性。
那到底是要用變異數還是標準差來描述這種嚴重性呢? 都一樣啦，標準差是變異數的平方根，看起來數字比較小，比較漂亮，比較無感而以啦。

變異數的公式如下 :

$\sigma ^{2} = \frac{1}{n}\sum_{i=1}^{i=n}(x_{i}-\mu )^{2}=\frac{(x_{1}-\mu )^{2}+(x_{2}-\mu )^{2}+…+(x_{n}-\mu )^{2}}{n}$

$\sigma$ 也唸成Sigma

import numpy as np
rng=np.random.RandomState(0) #偽亂數
d=rng.randint(1,100,10)
print(d)
u=d.mean()
o2=((d-u)**2).mean()
print('((d-d.mean())**2).mean() : ', ((d-u)**2).mean(), '<====變異數')
print('d.var() :', d.var(), '<====變異數')
print('標準差 : ', d.std(), '<===就是變異數的平方根')
結果 :
[45 48 65 68 68 10 84 22 37 88]
((d-d.mean())**2).mean() : 593.25 <====變異數
d.var() : 593.25 <====變異數
標準差 : 24.3567239176372 <===就是變異數的平方根

以平方差的姿態，加入群組之後，大量影響群組的結果，然後平圴群組的數字，造成差異。

標準差(Standard Deviation – SD)

就是變異數的平方根，如上所示

矩陣相乘

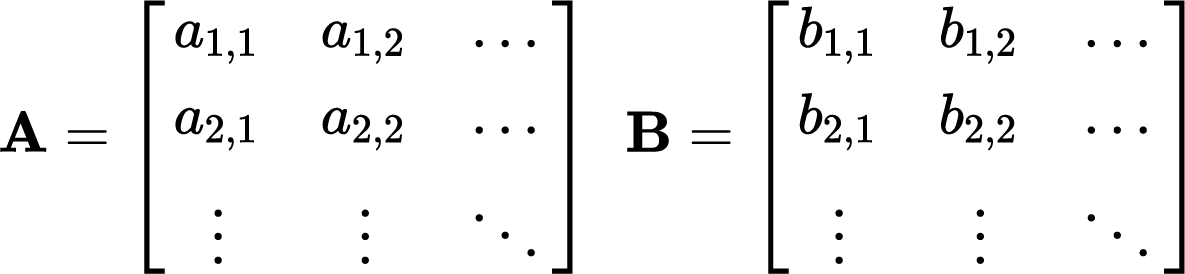
底下有一些數學矩陣計算式，再此先說明矩陣乘法

假設矩陣A為2*2，矩陣B為 2*3, 則A*B為2*3矩陣

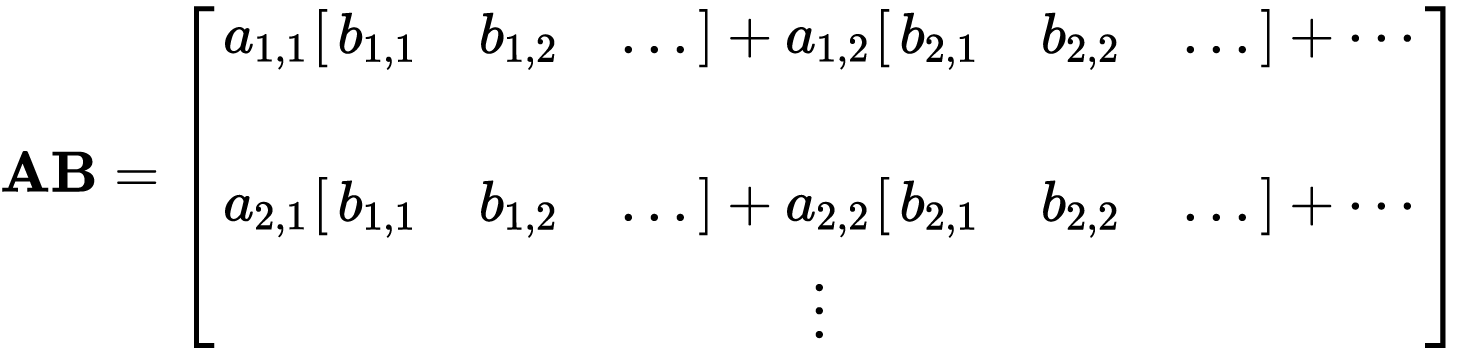
import numpy as np
a=np.array([[1,2, 3],
            [4, 5, 6]])
b=np.array([[1,2],
            [3,4],
            [5,6],
            ])
c=a @ b
print(c)

d=np.array([[1,2,3],
            [4, 5, 6]])
e=np.array([[1,1,1],
            [2, 2, 3]])
f=d*e
print(f)
結果
[[22 28]
[49 64]]
[[ 1 2 3]
[ 8 10 18]]

向量Vector

向量是方向的量化，或方向數位化的簡稱。描述方向的方式，可以用右上30度，左下45度。

這種描述的方式，對人類而言很直覺，但在數學或電腦上，無法計算。所以就量化成 x, y二軸的數字(3, 4)

todo

下圖紅色線 z 是由 x 及 y 二條綠色線組成。所以我們定義 $\vec{z}=\vec{x}+\vec{y}$

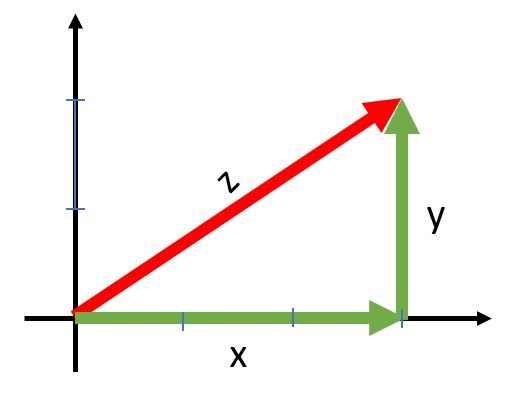
對於向量的寫法，總是有點難懂。把它想像成是一艘太空船，以水平3km/hr的速度往右，垂直2km/hr的速度往上。所以這艘太空船就會以$\sqrt{3*3+2*2}=\sqrt{13}$的速度往$\vec{z}$的方向前進。

基底向量

我們定義$\vec{i}=\begin{bmatrix}1\\0\end{bmatrix} , \vec{j}=\begin{bmatrix}0\\1\end{bmatrix}$

上述的$\vec{x}$及$\vec{y}$分別為

$\vec{x}=3 * \begin{bmatrix}1\\0\end{bmatrix}$

$\vec{y}=2 * \begin{bmatrix}0\\1\end{bmatrix}$

所以$\vec{z}=\vec{x}+\vec{y}=3*\vec{i}+2*\vec{j}$

$\vec{i}$及$\vec{j}$，我們稱為基底向量。以1為主的基底向量，稱為標準基底向量。此時有二個變數 3, 2，亦稱為二個特徵。

變更基底向量

如果上述的基底向量變更為
$\vec{v}=\begin{bmatrix}1.5\\1\end{bmatrix}$，此時$\vec{z}=2*\vec{v}$
若再變成
$\vec{v}=\begin{bmatrix}3\\2\end{bmatrix}$，此時$\vec{z}=1*\vec{v}$

也就是整個圖轉成如下的樣子，此時只需一個變數 “2” 或 “1” 即可描述整個向量。此時特徵就會變成只有一個

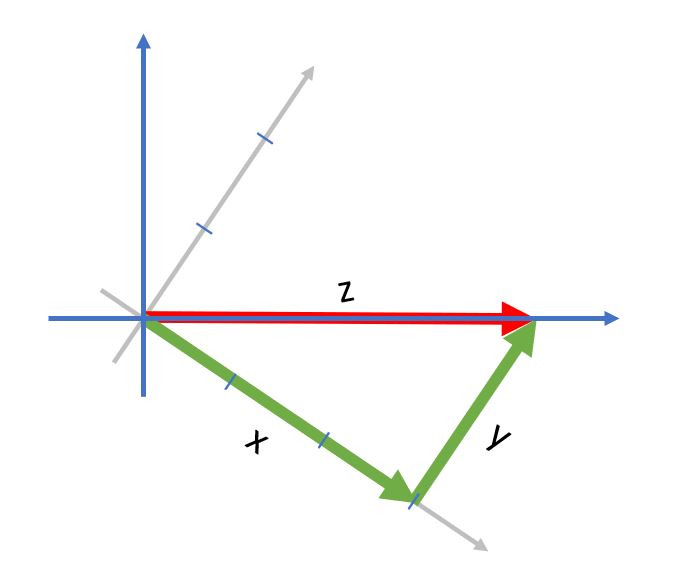
說的更直白一點，$\vec{v}$就是我們要巔覆傳統的度量衡單位，創造另一個新的單位。比如現今有一公尺，一公里。但我們就是要創造一個新的單位，比如~~一光秒(光一秒跑的距離)。那麼太陽離地球的距離就不再是1.5億(150,000,000)公里，而是500光秒，也就是8.3光分，如此簡化了很多個 “0”。

向量就是 2*1矩陣

上述不論是$\vec{v}=\begin{bmatrix}3\\2\end{bmatrix}$ 或是 $\vec{i}= \begin{bmatrix}1\\0\end{bmatrix}$
可以很明顯的看出，原來向量就是一個 2*1的矩陣$\begin{bmatrix} x\\y\end{bmatrix}$，也就是$\begin{bmatrix}x,y \end{bmatrix}^{T}$

張量(Tensor)

以圖片像素為例，每個像素皆有(r, g, b)三個值。我們稱每個點的(r, g, b) 為一個向量。而如下黃色區域每一個格點都有一個向量。這些眾多向量的集合，稱為張量。也就是說，張量是由多個向量組成。

說的更貼切一點，就是在二維平面上，每個點又有多個特徵的意思。拓展開來，m個維度上，每個點又有n個特徵

本章節出現在數學篇是為了講解微分的方法。
但在AI TensorFlow章節又重新列出，是為了講解梯次下降的方法。

二都關係密切，所以必需完全了解。

一元二次方程式求解

$ax^{2}+bx+c=0$

二邊除a : $x^{2}+\frac{bx}{a}+\frac{c}{a}=0$

$\therefore x^{2}+\frac{bx}{a}=-\frac{c}{a}$

二邊加上$(\frac{b}{2a})^{2}$  => $x^{2}+\frac{bx}{a}+(\frac{b}{2a})^{2}=-\frac{c}{a}+(\frac{b}{2a})^{2}$

$\therefore (x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}}$

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

導數

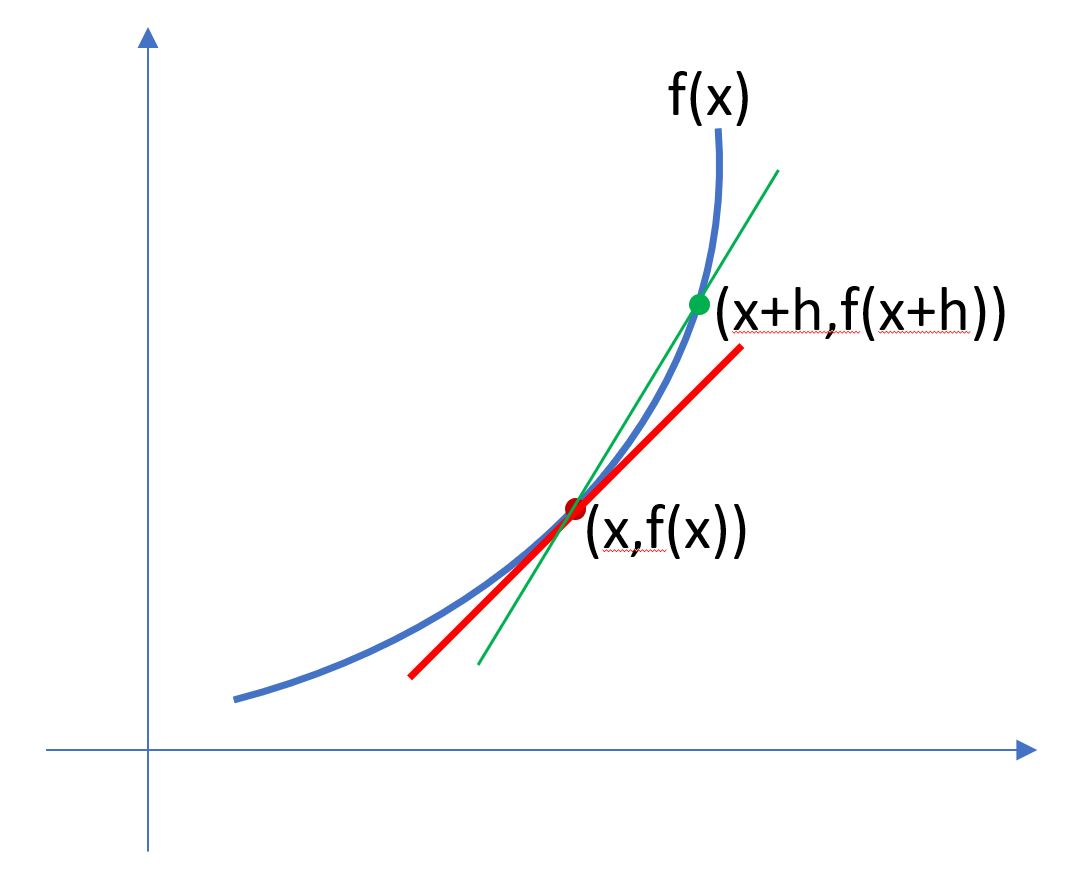
上圖藍色曲線的方程式，假設為 f(x)，則(x, f(x))這個點的切線(紅色線)斜線為多少呢?。

首先x往右邊增加一個h的值，其y軸為f(x+h)，所以綠色(割線)斜率為$\frac{f(x+h)-f(x)}{h}$

當h往左邊靠，一直逼近x時，那就是紅色線的斜率 $\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$

把上面的那個式子，給予一個變數 $f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$, 則$f'(x)$稱為導數
所以導數就是某個點的斜率。

假設$f(x)=x^{2}$，則斜率為

$\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^{2}-x^{2}}{h}=\frac{x^{2}+2xh+h^{2}-x^{2}}{h}=2x+h$

$f'(x)=\lim_{h\to0}2x+h = 2x$

也就是說，x=1時，斜率為2, x=2時，斜率為4

而$f'(x)=2x$ 正是 $x^{2}$的微分，也就是說，導數就是切線，也就是微分後的函數

偏微分

上述的方程式，只有一元變數(x)。如果是多元呢，如下所示

$f(x_{1},x_{2})=ax+1=\begin{bmatrix}10&1\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}+1=10x_{1}+x_{2}+1$

$\bigtriangledown f(x_{1},x_{2})=\begin{bmatrix}\frac{\partial f(x)}{\partial x_{1}} \\ \frac{\partial f(x)}{\partial x_{2}}\end{bmatrix}=\begin{bmatrix} \frac{\partial(10x_{1}+x_{2}+1))}{\partial x_{1}} \\ \frac{\partial(10x_{1}+x_{2}+1))}{\partial x_{2}} \end{bmatrix} =\begin{bmatrix} 10 \\ 1 \end{bmatrix}$

多次多元方程式偏微分

$f(x_{1}, x_{2})=5x_{1}^{2}+2x_{2}^{2}+7x_{1}x_{2}+10x_{1}+x_{2}+1$

偏微分後為 $f'(x_{1}, x_{2})=\begin{bmatrix} 10x_{1}+7x_{2}+10 \\ 4x_{2}+7x_{1}+1 \end{bmatrix}$

由上可推出，如果是2元方程式，就是2*1矩陣，如果是 3元方程式，就是3*1矩陣

梯度下降

梯度下降(Gradient Descent)，目的是在使用逼近法尋找最接近的函數

import numpy as np
import pylab as plt
px=[1,0, -1]
py=[1, 0, -3]

reg=np.poly1d(np.polyfit(px, py, 1))
plt.plot(px, reg(px), color='green')

x=np.linspace(-1.5, 1.5, 2)
y=3*x+1
plt.plot(x, y, color='red')

plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei']
plt.rcParams['axes.unicode_minus'] = False
plt.legend(['迴歸', '假設'] )
plt.scatter(px, py)
plt.plot([-4, 4], [0, 0], color='blue')
plt.plot([0, 0], [-4, 4], color='blue')
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.grid(True)
plt.show()

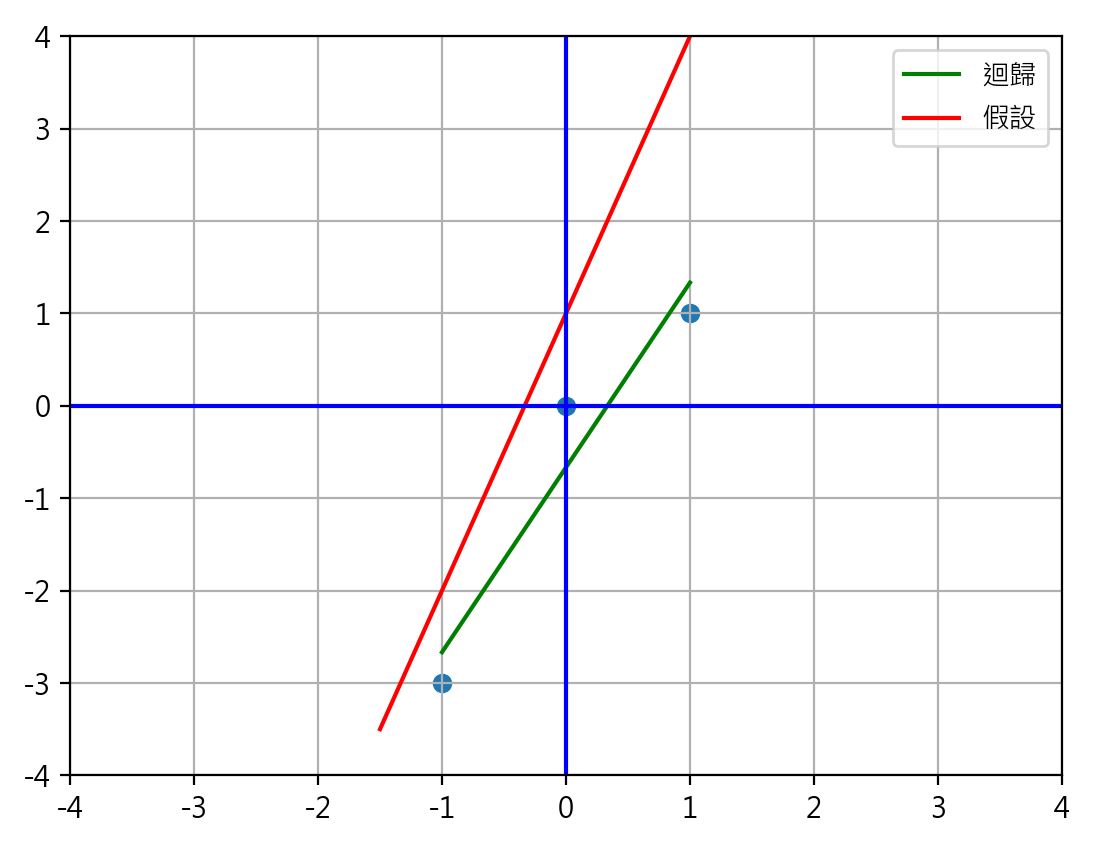
如上圖，假設有三個點(目標點)分別為(1, 1), (0, 0), (-1, -3)。如果我們要找一條線最接近這三個點。依以前的想法，那就是綠色那條迴歸線了。但迴歸線又是怎麼找出來的呢?
在此我們先隨便假設一條線，如紅色的 f1(x)=3x+1 這個函數。然後把三個點的x值代入f1函數，得到的y值如下

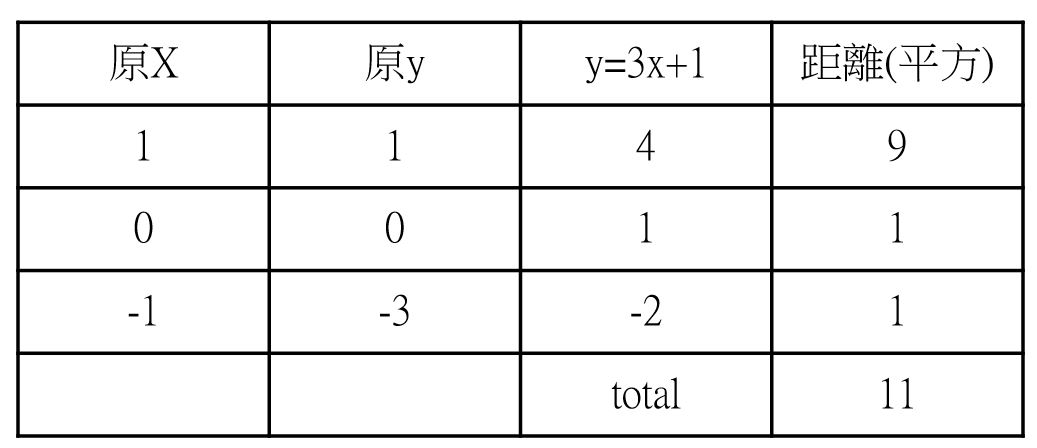
上述3x+1所求出的y值，與目標點的y值相減後的平方，加總為11。為什麼要平方呢? 這樣才不會有負值出現. 即總距離為
$\sum_{i=0}^{i=n}(y_{ni}-y_{oi})^{2}$ 
$y_{ni}$ 為目標點的y值，$y_{oi}$ 為目標點的y值

這樣可以解釋迴歸線跟PCA的差異了吧。PCA是三點的投影距離總和的最小值。迴歸線是三點的y值與原點最小總值。

再以上例$f(x)=x^{2}-10x+1$為例，x為多少時，有最小極值呢。用上述的一階微階可知 $f'(x)=2x-10$，當x=5時，表示斜率為0，有極值，所以f(5)=-24。但較複雜的函數並不是都可以使用此方法求值。此時就要用逼進法(梯度下降)。

再以上述$x^{(t+1)}=x^{t}-\gamma f'(x^{(t)})=x^{t}-\gamma (2x^{(t)}-10)=(1-2\gamma )x^{(t)}+10\gamma$
$\gamma$ : 學習函數，每次要進步的值
$x^{{t}}$ : 當下x的值
$x^{{t+1}}$ : 下一次x的逼進值

$\gamma$ 的值複雜亦常，太大也不行，太小也不行，這又有一套理論，所以可以先跳過

損失函數

再以$f(x)=x^{2}-10x+1$為例
$L=\sum (y-(x^{2}-10x+1))^2$, 即 (目標點y-新點y)的平方總和。

加速度

距離與加速度的公式為 : $S=v_{0}t+\frac{1}{2}at^{2}$

對t 進行一次微分後，就是某個時間點的瞬間速度了

$v=v_{0}+at$

https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E6%B7%B1%E5%BA%A6%E5%AD%B8%E7%BF%92-%E5%9F%BA%E7%A4%8E%E4%BB%8B%E7%B4%B9-%E6%90%8D%E5%A4%B1%E5%87%BD%E6%95%B8-loss-function-2dcac5ebb6cb

時間膨脹公式

速度愈快，時間膨脹愈大

$r=\frac{1}{\sqrt{1-(\frac{v}{c})^{2}}}$

todo

牛頓第二定律

F=ma

F:力量(N)，m : 質是(kg)，a: 加速度

todo

重力計算公式

g = $\frac{G*M}{r^{2}}$

g: 重力加速度，G: 重力常數，M : 星球質量，r:離地心距離。

G = $6.6743  * 10^{-11} \frac{m^3}{kg.s^2}$，此為固定不變

地球質量 : $5.97 * 10^{24}$kg，太陽質量 : $1.98855 * 10^{30}$kg

地球半徑: $6.371 * 10^{6}$m，太陽半徑: $6.955*10^{8}$m

地球表面重力加速度 = $\frac{(6.6743  * 10^{-11})*(5.97*10^{24})}{(6.371 * 10^{6})^{2}}$ =9.8 $m/s^{2}$。

太陽表面重力加速度 = $\frac{(6.6743*10^{-11})*(1.98855*10^{30})}{(6.955*10^{8})^{2}}$=274.3$m/s^{2}$

重力時間膨脹

重力也會讓時間變慢，公式如下

$t=1+\frac{gh}{c^2}$

g=9.8
h=1000km=10^6m
c=299792458
t=g*h/(c**2)*(10**9)
則位於高空1000km處的衛星，時間會比地表快 0.11奈秒

todo

史瓦西半徑

$r=\frac{2GM}{c^2}$

任何具有質量的物質都存在的一個臨界半徑特徵值。該值的含義是，如果特定質量的物質被壓縮到該半徑值之內，將沒有任何已知類型的力可以阻止該物質將自己壓縮成一個奇異點，也就是黑洞。在物理學和天文學中，尤其在萬有引力理論、廣義相對論中，它是一個非常重要的概念。這是1916年德國天文學家卡爾·史瓦西首次發現史瓦西半徑的存在，這個半徑是一個球狀對稱、不自轉又不帶電荷的物體。史瓦西半徑為這個物体的重力場精確解。

以太陽為例

$r=\frac{2*(6.6743*10^{-11})*(1.98855*10^{30})}{299792458^2} = \frac{2*(1.98855*10^{30})}{(6.6743*10^{11})*299792458^2} = 2953.4m$

也就是說，太陽在坍塌到 2953 公尺後，即會變成一個黑洞。地球則必需坍塌到0.8cm才會變成黑洞。