熟記
args=np.polyfit(x, y, n):產生n階方程式的參數
f=np.poly1d(args):產生n階方程式
f=np.poly1d(np.polyfit(x,y,n)):簡寫法
y=f(x):產生y的值
迴歸線定義
多個點中,尋找一條線,此線與每個點的 y 軸距離平方總和為最小值,那此條線就稱為迴歸線。如下圖,所有紅色線的長度(上為正,下為負)的平方加總後,若得到最小值,那麼那條線就是迴歸線。
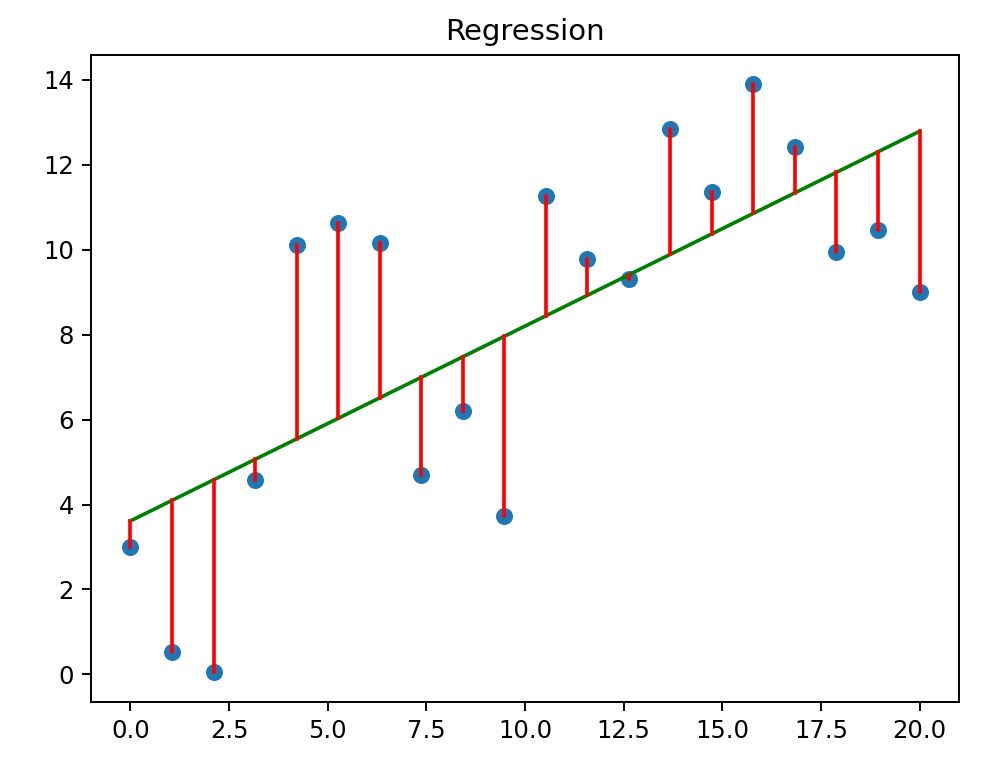
線性迴歸的運作原理
自然界有很多定律, 永遠打不破. 比如高鐵以恒速300km跑二小時, 那跑出的距離就是 s=v0t=300*2=600km.
等等, 牛頓定律不是說 s=v0t+1/2at2 嗎. 嗯, 沒錯. 但剛剛說了, 是以”恒速” 在跑, 也就是說沒有加速度的情形下, a =0. 在這種可以用公式算出來的東西, 其實是最簡單的預測. 但嚴格來說, 不能說是預測, 而是絕對會發生.
線性迴歸英文為 linear regression [rɪˋgrɛʃən] . regression的中文是退化的意思. 所以線性迴歸的作用, 是在一群資料中, 找到一條直線或曲線.
舉個例子. 近來溫室效應的關係, 天氣溫度愈來愈熱. 溫度與農作物產量有關, 溫度愈高, 農作物產量愈少. 但並不是高了一度, 就會少幾頓這麼精準, 而是會在一定範圍中上下跳動. 而我們人類的眼睛所看到的, 就是會一直往下降 (其實這也是物理學的測不準原理).但會降多少呢, 不一定, 只是會降在一定的範圍值之內.
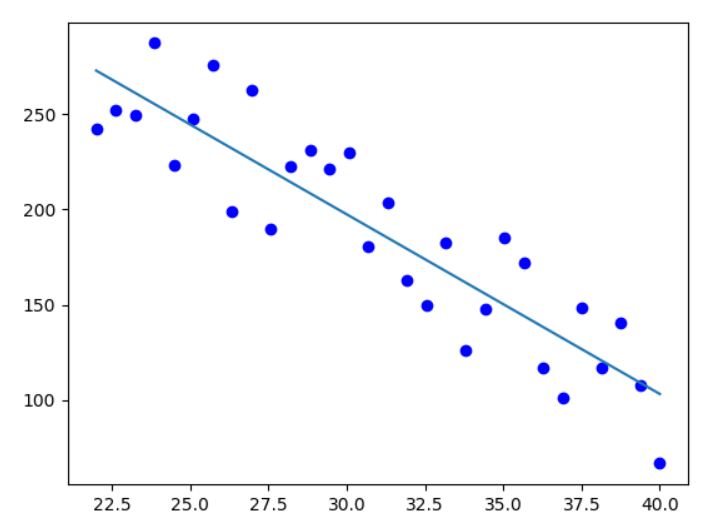
下圖中, x軸表示溫度(oC), y軸表示產量(噸). 當溫度逐漸往右升高時, 產量就持續往下降
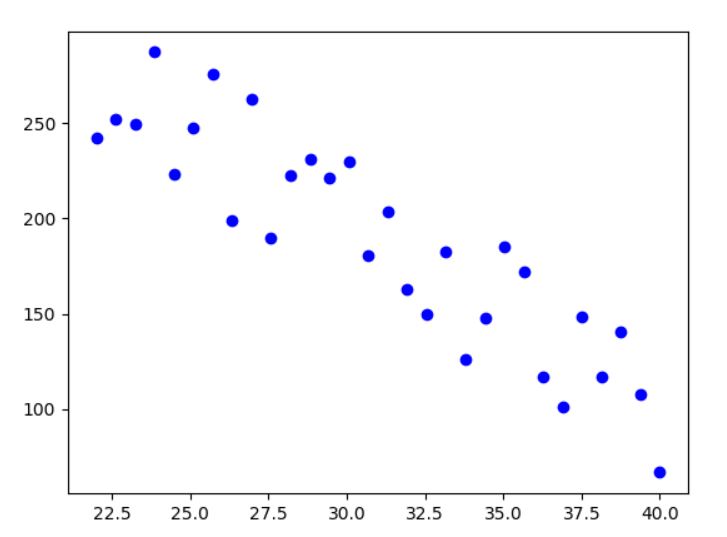
上圖的代碼如下
import numpy as np import matplotlib.pyplot as plt n=30 temperature = np.linspace(22,40,n) #產出 [22,23,24,....40] 共 30個數字 noise=(np.random.random(n)*2-1)*40 value = 500-temperature*10+noise plt.plot(temperature, value, "bo") plt.show()
在這些雜亂的數值中, 畫出一條線, 作為日後參考的依據. 這就好比退化或簡化成一條線, 這就是線性迴歸的功能.
下面代碼中, 藍色部份 np.polyfit(), 會產生args tuple, 裏面有二個參數分別為 args[0] 及 args[1], 這二個參數可以擬合 temperature 及 value這些資料而製作出一階方程式 y=args[0]*x+args[1]. 這個一階方程式即為回歸直線
import numpy as np import matplotlib.pyplot as plt n=30 temperature = np.linspace(22,40,n) noise=(np.random.random(n)*2-1)*40 value = 500-temperature*10+noise plt.plot(temperature, value, "bo") args=np.polyfit(temperature,value,1) y=args[0]*temperature+args[1] plt.plot(temperature, y) plt.show()
多階回歸線
上述回歸線為直線, 屬於一階方程式, 其實不需要自行撰寫 y=args[0]*temperature+args[1], 可以直接使用 f1=np.poly1d(args)產生一階公式, 然後就再使 y=f1(temperature)產生線性資料.
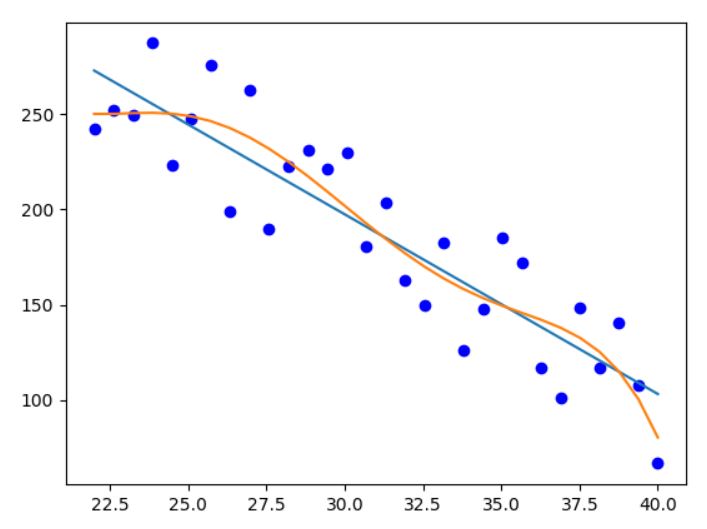
如下代碼, 即產生5階參數, 再產生5階曲線, 再求曲線值
f1=np.poly1d(np.polyfit(temperature,value,1)) f5=np.poly1d(np.polyfit(temperature,value,5)) plt.plot(temperature, f1(temperature)) plt.plot(temperature, f5(temperature)) plt.show()
股市分析
此分析資料涉汲本人伺服器帳密問題, 所以非課堂上的讀者請由如下練習
請注意, 線性迴歸只能適用於自然界非人為因素的預測. 其實就算自然界也會因為地震天災造成不準確性, 更何況是人為因素.
而股市不僅僅有人為因素的介入, 更是一個合法的詐騙集團. 若硬要把回歸線套入股票分析, 只能得一結論, 絕對不會準確.
下面的代碼, y值為台灣4, 5, 6, 7月四個月份的大盤指數, 其趨勢圖如下
import pylab as plt import numpy as np x=np.linspace(1,84,84) y=np.array([ 10714.68,10695.47,10725.17,10759.96,10805.39,10839.93,10869.24,10820.94,10849.84,10905.63,10961.61,11038.24,11017.69,10994.52,10994.28,11054.02,11017.73,10986.53,10952.91,10945.94, 10992.76,11037.99,11005.36,10913.95,10938.47,10910.47,10751.55,10684.04,10480.21,10535.24,10556.58,10508.56,10405.36,10362.35,10481.10,10404.00,10313.15,10344.18,10348.58,10277.35,10307.12,10386.12, 10482.45,10499.51,10497.50,10409.90,10486.23,10567.54,10605.75,10582.19,10546.42,10488.70,10547.15,10650.48,10749.41,10817.71,10734.25,10777.18,10661.39,10674.20,10786.66, 10821.30,10878.01,10793.10,10755.87,10785.85,10742.81,10729.83,10723.23,10817.60,10855.16,10819.92,10865.00,10861.11,10821.92,10861.99,10910.50,10963.86,10969.74,10892.25,10898.25,10872.63,10909.98,10824.15]) f2=plt.poly1d(plt.polyfit(x,y,10)) y2=f2(x) plt.figure(figsize=(12,6)) plt.plot(x,y,"bo") plt.plot(x,y2) plt.show()
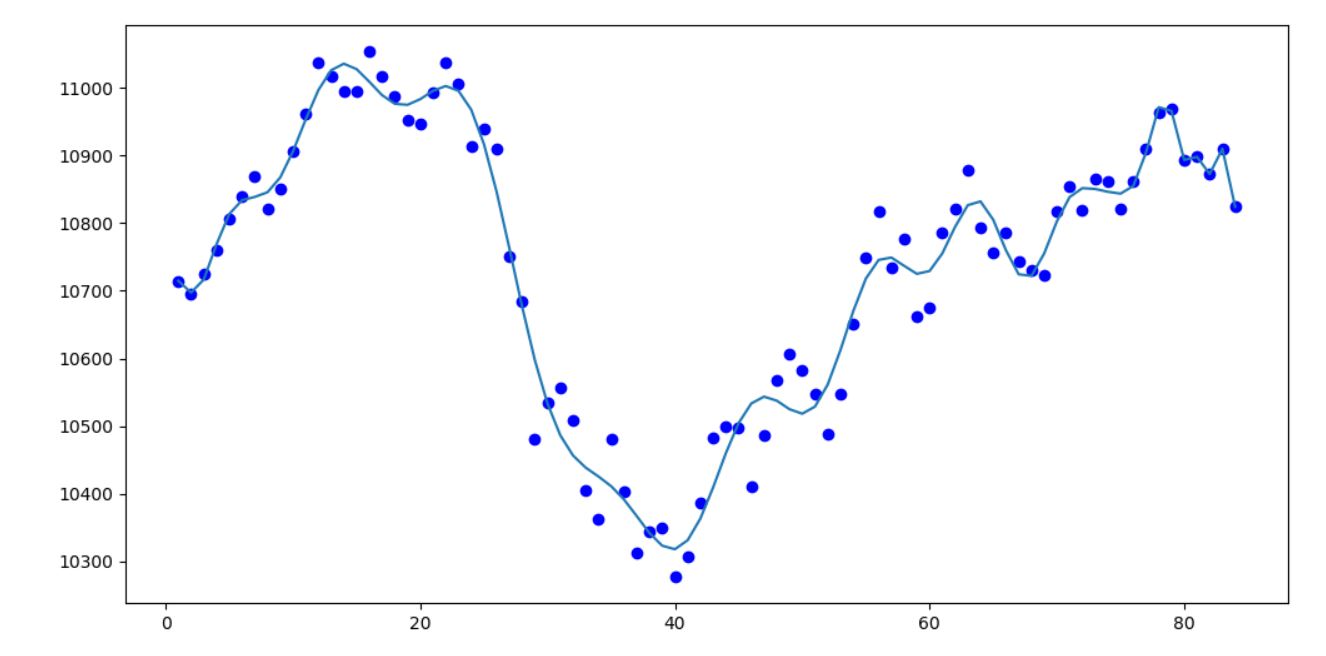
若是課堂上的讀者, 請由如下練習, 帳密會於課堂上說明
import pylab as plt
from matplotlib.font_manager import FontProperties
from datetime import datetime
import matplotlib.dates as mdates
import mysql.connector as mysql
conn=mysql.connect(host="ip",user="account", password="pwd", database="db")
warehouse = {}
d=datetime.now()
cmd="select * from taiex where tx_date >= '2016/01/01' and tx_date<='{0}/{1}/{2}'".format(d.year, d.month, d.day)
cursor=conn.cursor()
cursor.execute(cmd)
rows=cursor.fetchall()
y=[]
x_date=[]
for row in rows:
y.append(row[5])
x_date.append(row[1])
font = FontProperties(fname=r"C:/WINDOWS/Fonts/simsun.ttc", size=16)
plt.figure(figsize=(12,6))
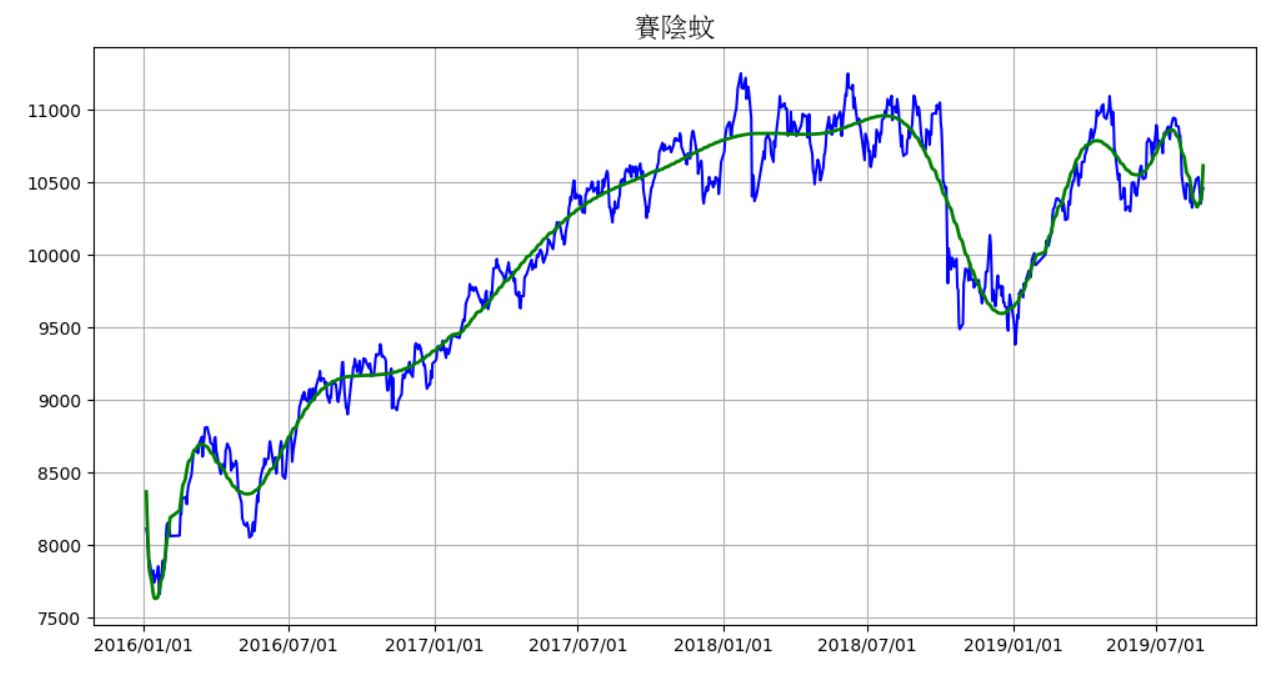
plt.title("賽陰蚊", fontproperties=font)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d'))
plt.plot(x_date,y, color='blue')
x=list(range(len(y)))
f=plt.poly1d(plt.polyfit(x, y, 20))
plt.plot(x_date, f(x), color='green', linewidth=2)
plt.grid()
plt.show()