二維

在二維的平面上，任何一條曲線都可以用 1 元 n 階方程式來表示，

比如 $(y=0.001x^6-0.1x^5-0.68x^4+10000x^2+2)$

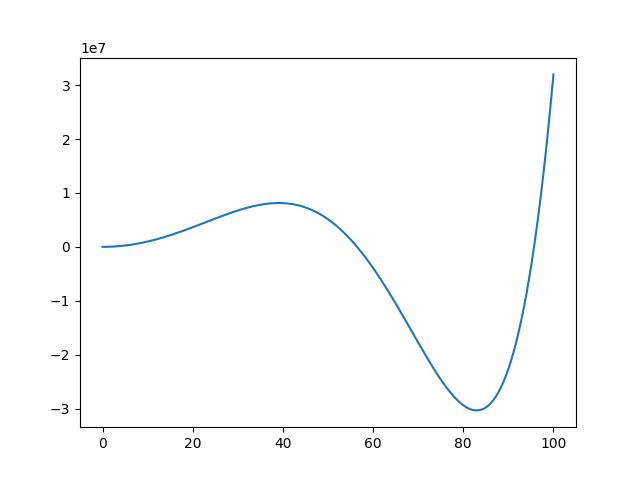
上面的公式，y 是結果，x 是變數。變數 x 只有一個，稱為 1 元，x 變數最大是 6 次方，稱為 6 階。所以形成下面的圖示。

import numpy as np
import pylab as plt
x=np.linspace(0,100, 10000000)
y=0.001*(x**6)-0.1*(x**5)-0.68*(x**4)+10000*(x**2)+2
plt.plot(x,y)
plt.show()

三維

那麼在三維空間上，就可以使用 2 元 n 階來表示任何一個平面， z 是結果，x 及 y 是變數 (2元)，比如

$(z=ax^4+by^4+cx^3+dy^3+ex^2+fy^2+gx+hy+i)$。

ps : a, b, c, d, e, f, g, h, i  是常數

底下是 $(z=\frac{0.006x^6-0.005y^6+0.5x^5-0.1y^5+0.005x^4+0.003y^4}{10000000})$ 所展示出來的平面。

import plotly.graph_objs as go
import numpy as np
import pandas as pd
import plotly
z=np.zeros([100,100])
for x in range(0,100):
    for y in range(0, 100):
        z[x, y]=(0.0006*x**6-0.005*y**6+0.5*x**5-0.1*y**5+0.005*x**4+0.003*y**4)/10000000
#df=pd.DataFrame(data=z)
trace=go.Surface(z=z) # 將dataframe所有的值以list列出
data=[trace]
layout=go.Layout(title='3D', autosize=True,
                  margin=dict(l=50, r=50, b=50, t=50))
fig = go.Figure(data=data, layout=layout)
fig.show()
#plotly.offline.plot(fig, filename="3d.html", auto_open=True)

底下的地型圖，也可用 2 元 n 次方程式來表示，不過這個方程式非常猙獰，甚至複雜到非常的長。

多維

那麼如果是四維，五維，六維呢，因為變數太多了，所以就用 $(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, ….)$ 來命名變數名稱，然後用 y 表示結果。

$(y=ax_{1}^5+bx_{2}^5+cx_{3}^5+….)$