對函數進行微分的目地就是求取切線的斜率。

其實這個不好懂，所以換個角度來思考。牛頓告訴我們，當有加速度時，瞬間速度的公式是 $(v=at)$，v 是速度，a 是加速度(感受一下加速度，當車子一加速，人會往後傾，油門加愈大，感覺往後傾的力道愈大)，t 是時間。

比如 a=2，那就是每秒鐘增加 2 m/s 的速度，第 0 秒的速度是 0 m/s，第 1 秒的速度是 2 m/s，第 2 秒的速度是 4 m/s， 那麼第 10 秒的速度就是 20 m/s。

再思考一個問題，第 1 秒車子會移動到多少公尺 ? 第 2 秒車子會到那裏? 公式是 $(S=\frac{1}{2}at^{2})$。如下的程式

import pylab as plt
import numpy as np
t=np.linspace(0,10,100)
a=2
v=a*t
S=(1/2)*a*t**2
fig, axes=plt.subplots(1,2, figsize=(12,6))
axes[0].plot(t, v)
axes[0].set_title("Speed")
axes[0].set_xlabel("Time")
axes[0].set_ylabel("Speed")
axes[1].plot(t, S)
axes[1].set_title("Distance")
axes[1].set_xlabel("Time")
axes[1].set_ylabel("Distance")
plt.savefig("accele_1.jpg")
plt.show()

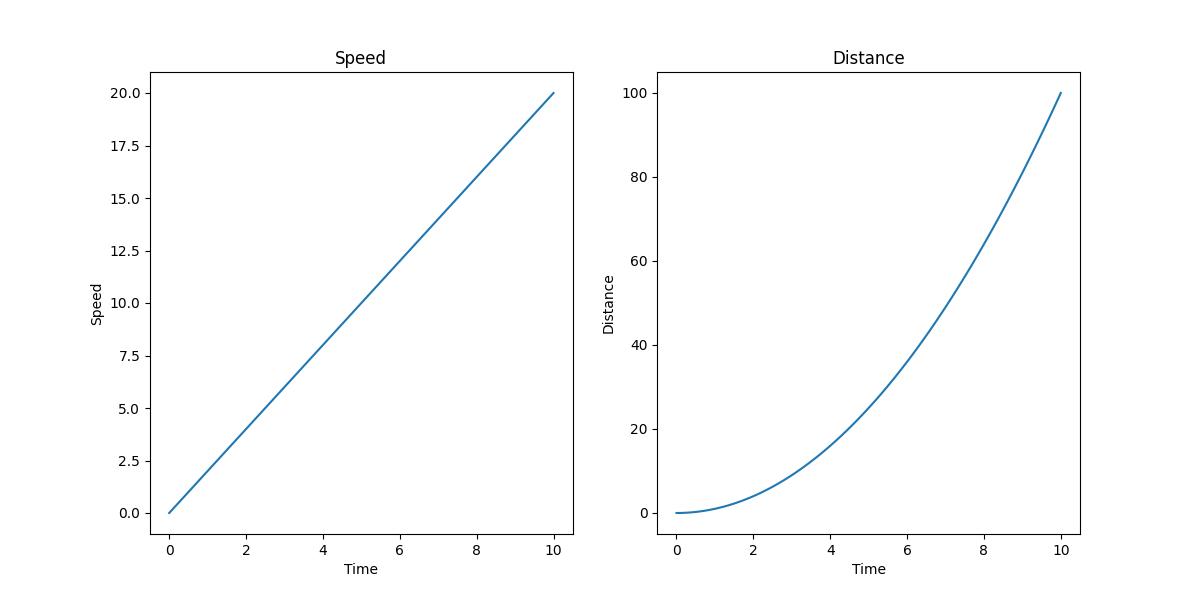
上面右邊的圖，可以看到 x 軸是 time，y 軸是距離，而 $(S=\frac{1}{2}at^{2})$ 微分後產生的那一個直線斜率就是速度，也就是 $(v = at)$。

那麼換成 $(y = \frac{1}{2}ax^{2})$ 呢，那麼請問微分後 $({y}’ = ax)$，這個 $({y}’)$  是什麼? 我們都知道 $({y}’)$ 是斜率，但這斜率到底代表著什麼意思?? 一頭霧水，所以沒有物理學的運動定律公式就很難理解。

找極值

微分用在尋找一元二次方程式的極值相當好用，以下使用一個函數說明

$(f(x)=x^{2}-10x+1)$。若使用Python來畫出其函數圖形，如下

import numpy as np
import pylab as plt
x=np.linspace(-10,20, 30)
y=x*x-10*x+1
plt.plot(x, y)
plt.show()

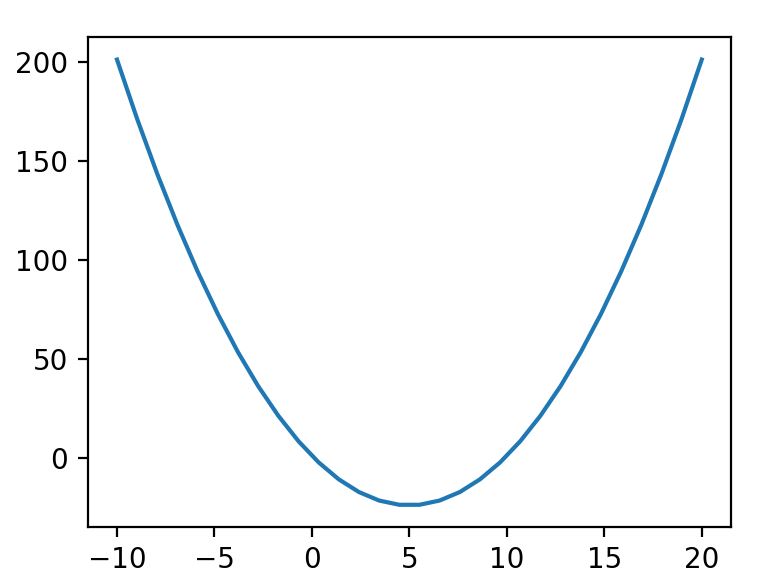
上圖為$(f(x)=x^{2}-10x+1)$函數的圖形。在x差不多是5的時候，有最小的 y值。所以有二個問題
1. 當x為多少時，有最小的y值?
2. 最小y值又是多少?

依導數的說明，可知道當切線斜率為0時(水平線)，y有極值。所以先一階微分求其斜率函數
$(f'(x)=\frac{\partial f(x)}{\partial x}=2x-10)$

1. 當一階微分為0時，也就是斜率為水平線，y有極值，即$(2x-10=0)$, x=5
2. y的極值為 5 * 5 – 10 * x + 1 = -24

極大還是極小

上述求出的極值 -24，是極大還是極小呢?

此時再進行二階微分，若值 >0，則此 y 值為極小值。若值 <0，則此 y 值為極大值
$(f”(x)=\frac{\partial f'(x)}{\partial x}=2 >0)$，所以 -24 為極小值

偏微分

在二維座標中，y 是值(結果)，變數只有 x，稱為一元 n 階方程式。y 對 x 的微分，是求取 x 在 x 點時的斜率。

在三維中，z 是值(結果)，變數有 x 及 y 二個，稱為二元 n 階方程式。z 對 x 的微分稱偏微分，當然 z 對 y 的微分也稱偏微分。