蒙地卡羅方法 (Monte Carlo method)又稱 統計類比方法，於1940年因電腦問世而發展出一種以機率統計數值的計算方法。

在電腦的世界，就是要想盡辦法將類比轉成數位。而蒙地卡羅反其道而行，要將數位轉換成類比。此法使用亂數 (偽亂數) 來解決很多計算問題的方法。

蒙地卡羅方法是為了核武計劃所產生的一個演算法，由科學家馮·紐曼、斯塔尼斯拉夫·烏拉姆和尼古拉斯·梅特羅波利斯於洛斯阿拉莫斯國家實驗室發明。烏拉姆的叔叔經常在摩納哥的蒙地卡羅賭場輸錢，故以此地命名。

蒙地卡羅方法常運用在金融工程學、總體經濟學、生物醫學、計算物理學 (如粒子輸運計算、量子熱力學計算、空氣動力學計算)、機器學習等領域。

求 $(\pi)$ 值

蒙地卡羅方法使用學術名詞來講解的話，的確是艱深難懂。所以本篇不講學術理論，直接使用數學圓周率 $(\pi)$ 值求法來解釋其用途。

小學的數學老師總是教我們圓面積的公式為 $(\pi r^{2})$，然後叫我們要把 $(\pi = 3.14159265)$ 這個數字背起來，但從來都沒有講 3.14159265 這個數字是怎麼來的。

本人深刻記得小學老師補了一句話~~”這個 $(\pi)$ 值必需到了上大學時，學會高等數學才能求的出來，你們現在無法懂，所以必需背下來”。

底下我們也不使用高等數學求$(\pi)$值，而是使用蒙地卡羅法 (Monte Carlo method) 求取 $(\pi)$ 值。

原理

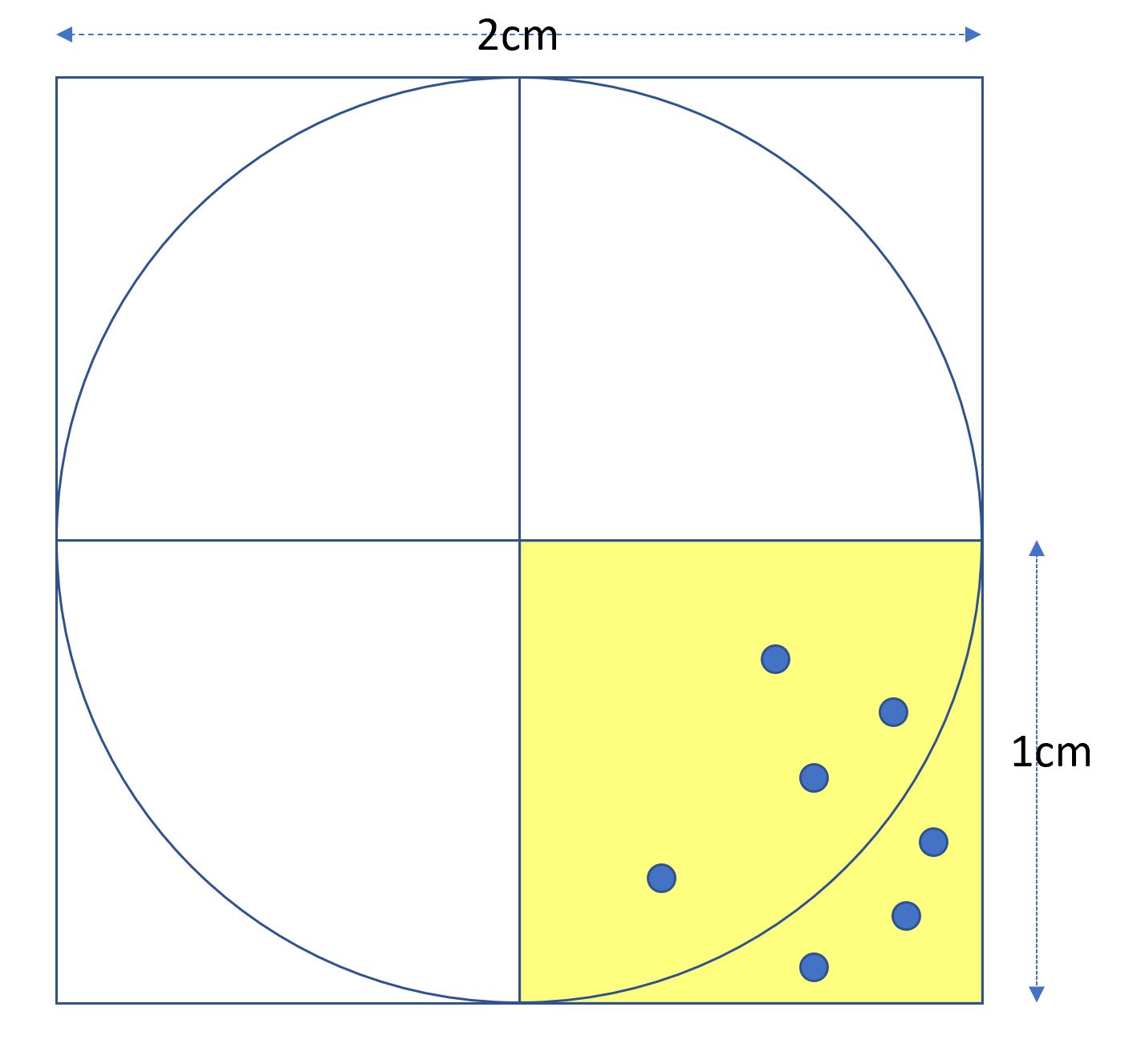
如下圖示，假設有一個正方型，長寬皆為2cm，中間有一個圓，直徑也為 2cm。為了方便計算，我們只專注右下角那個區塊，也就是黃色的部份。黃色區塊面積為 $(1cm^2)$，而1/4圓面積為 $(\frac{\pi r^{2}}{4} = \frac{\pi}{4})$

首先在右下角中產生 n 個亂數點，然後計算亂數點在圓內的數量(x)及 n 的比例 (area=x/n)，這個比例就是圓的面積。也就是說 $(area=\frac{\pi }{4})$，因此 $(\pi = area*4)$。

由上可知，n 的數值愈大，求出的 $(\pi)$ 值就會愈準確

底下代碼每次 (epoch) 產生 1億 (batch) 個點，然後計算 Epoch 200次，也就是總共計算 200 億個點。Epoch 不用設太大，因為每次產生1億個亂數就要花費約 0.5 秒以上，然後再計算 1 億個點又要花費約要 0.5 秒以上，200 次就要 200 秒以上。

本代碼由本人開發，效能更高更精準，若要連結，請註明出處~ mahaljsp。

import time
import numpy as np
def dist():
    points=[np.random.uniform(0,1,batch),
            np.random.uniform(0,1,batch)]
    d=np.sqrt(np.square(points[0])+np.square(points[1]))
    idx=np.where(d<=1)
    return idx[0].shape[0]
batch=10_000_000
epochs=200
incircle=0
for e in range(epochs):
    t1=time.time()
    incircle+=dist()
    t2=time.time()
    a=incircle/((e+1)*batch)
    print(f'epoch:{e+1}, {t2-t1:.6f}秒, pi={4*a:.6f}')
結果:
epoch:1, 0.451294秒, pi=3.142604
epoch:2, 0.534373秒, pi=3.142168
epoch:3, 0.521374秒, pi=3.142024
epoch:4, 0.502459秒, pi=3.141870
epoch:5, 0.480804秒, pi=3.141894
    CPU Epoch:004 =>1.95577秒, pi=3.14159577

上述執行一段時間後，會得到如下的結果

CPU Epoch : 200 pi=3.1416053336

規則

蒙地卡羅方法就是要找到規則，也就是說在什麼狀況屬於那一類。比如半徑小於等於 1 就是在圓內，大於 1 就是圓外。

總結

蒙地卡羅方法其實就是隨機灑入極大量的點 (可以想成是原子)，然後計算各種狀況的點數，進而分析其中的機率。而這個 “各種狀況”，就如上述的圓內或圓外。

可以想像抓一把沙子，然後灑在一定的範圍內，計算有幾顆沙子在圓內，幾顆沙子在圓外。還好，電腦計算沙子數量的能力，比人腦快了千萬倍。如果用人腦來算，10個人應該會有11個人變成神經病。

即然我們可以在短時間(幾天內)計算出 50萬 * 1億個數量，那麼計算核武裏中子的運作，當然不是問題，難怪這東西是因為核武而產生。

蒙地卡羅方法又稱 統計類比，其實就是將數位轉換成類比的方法。借由數位方式產生大量的數值，達成類比的效果。只不過 1940 年代，那時的電腦沒這麼快，可能要用好幾萬台電腦共同運算才能達到我們現在電腦的能力。歷史可以借鏡，若以現在的電腦速度，然後同時用 1000、10,000、100,000 台電腦來計算呢!!

未來 10~50 年的電腦運算能力可能比現在又高了上萬倍，一台比上萬台電腦，這又是一個新的領域了。

改進

蒙地卡羅採用平均亂數進行統計，但再怎麼平均也不會是真的平均，所以還是有改進的空間。

我們的改進法，是在 1*1 的面積裏，平均分割為 500 萬 * 500 萬的格子，然後計算每一個格子的半徑。統計半徑小於1 的數量。

import os
import time

import numpy as np

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
batch=10_000_000
incircle=0
xs=tf.linspace(tf.cast(0., dtype=tf.float64),1., batch)
ys=tf.linspace(tf.cast(0., dtype=tf.float64),1., batch)
total_time1=time.time()
for i, x in enumerate(xs):
    t1=time.time()
    dist = tf.sqrt(tf.square(x) + tf.square(ys))
    incircle=incircle+tf.where(dist<1).shape[0]
    pi=incircle/((i+1)*batch)*4
    t2=time.time()
    if i %100==0:
        print(f"\rEpoch:{i:,}=>{t2-t1:.5f}秒, pi={pi}", end="")
print()
total_time2=time.time()
print(f"\r總花費:{total_time2-total_time1}秒, pi={pi}", end="")
結果 : 
Epoch:9,999,999=>0.00100秒, pi=3.1415924251788
總花費:13960.736736297607秒, pi=3.1415924251788

蒙地卡羅 np 版

求 $(\pi)$ 值

原理

規則

總結

改進

發佈留言