小學的數學老師總是教我們圓面積的公式為 $(\pi r^{2})$,然後叫我們要把 $(\pi = 3.1415926)$ 這個數字背起來,但從來就沒有講為什麼是這個數字。
本人還記得小時候老師有補一句話~~這個 $(\pi)$ 值必需使用大學的高等數學才求的出來,你們現在也聽不懂,所以必需背下來。
底下我們就用高等數學的蒙地卡羅法 (Monte Carlo method) 求取 $(\pi)$ 值。
原理
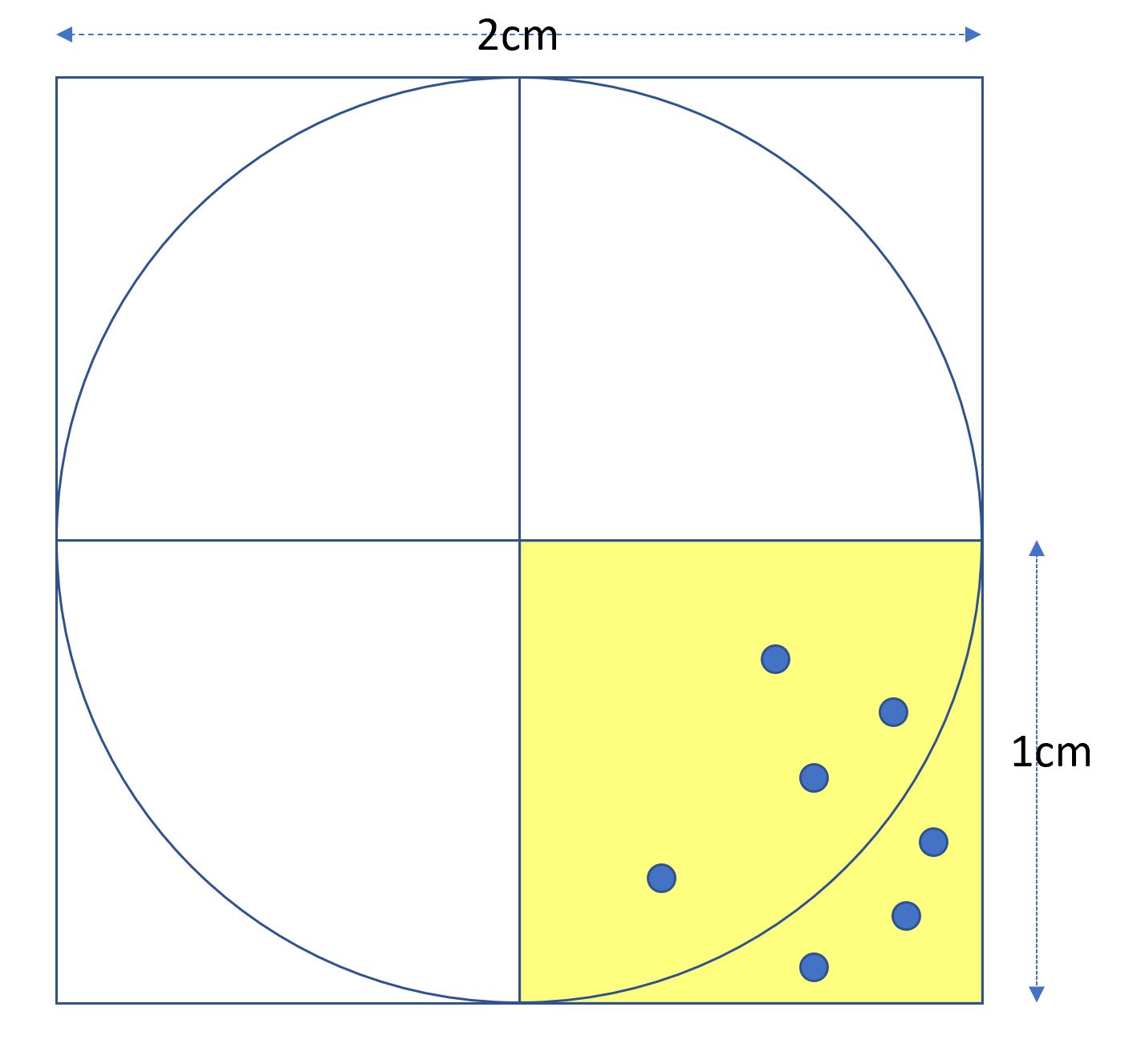
在如下圖示中,假設有一個正方型,長寬皆為2cm,中間有一個圓,直徑也為 2cm。為了方便計算,我們取右下角那個方塊,及1/4圓來計算。右下角方塊的面積為 $(1cm^2)$,而1/4圓面積為 $(\frac{\pi r^{2}}{4} = \frac{\pi}{4})$
首先在右下角中產生 n 個亂數點,然後計算亂數點在圓內的數量及 n 的比例 (area),這個比例就是圓的面積。也就是說 $(area=\frac{\pi }{4})$,因此 $(\pi = area*4)$。
由上可知,n 的數值愈大,求出的 $(\pi)$值就會愈準確
完整代碼如下
#include <iostream>
#include <cmath.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
bool circle(double x, double y){
double r=pow(pow(x,2)+pow(y,2), 0.5);
if (r<=1)return true;
else return false;
}
int main(){
srand(time(NULL));
unsigned long total=4000000000;
cout<<total<<endl;
unsigned int count=0;
for(int i=0;i<total;i++){
double x=rand()/(double)RAND_MAX;
double y=rand()/(double)RAND_MAX;
if (circle(x, y))count++;
}
double area=count/(double)total*4;
printf("%f",area);
}
上述執行一段時間後,會得到如下的結果
4000000000 3.141522
