大數據分析是外行人所杜撰的一個鳥名詞，其實就是統計學。統計學就是運用千萬種演算法來統計跟分析一大堆資料。只不過改由電腦來執行時，就被順便改名為大數據分析。

不懂統計學，能學會大數據嗎，再問就去跳海投胎啦，不然本篇是寫假的嗎!!

演算法千萬種，宇宙又浩瀚無窮，那些天文學家如何運用這些演算法來分析這宇宙? 放心啦，他們也是集千萬人的腦力，把演算法放在電腦中，需要時再拿出來算一算。如果什麼都要詳細明瞭，等於逼近神的領域。如何把千萬人的研究集中保存並方便計算，這才是深度學習的重點。

但是基本統計學必需要懂，如果不知加減乘除，你會知道什麼叫開根號嗎?!

後記~~
30年前逢甲大學青澀年代，本人就跟底下這本書結下樑子，因為曾被這本書當掉重修。時過30個年頭，回看這本大學用書，真的是垃圾，裏面的內容只是英文翻中文，完全沒有專業的解說，只比現在 Google 翻譯好了那麼一點點。

統計學(Statistics)

Statistics [stəˋtɪstɪks] 叫統計學，由歷史所留傳下來的一大堆資料，進行分析，找到其中的關連性，進而預測未來會發生的事。

要分析這些資料，需使用許多的手法(演算法)，這些手法，都是統計學的領域。

預測未來會發生的事?? 那這跟八字算命有啥不一樣? 八字算命本來就是統計學其中的一門 “科學”。

老實說，以前電腦還沒普遍，速度沒那麼快時，光是數字用手工加總就超費時的，更何況還要驗算這些演算法的正確性。難怪本人30年前大學時期的統計學會被當的原因，因為實在搞不懂這些是要幹什麼。

現在電腦普及了，更是佩服發明統計學的那些人，真的是天才。

奇數中位數(Median)

中位數，英文叫median [ˋmidɪən]，請熟記起來。

一組數字的數量如果是奇數，比如有 3 個數字，將這 3 個數字由小到大排列，然後取中間那個數，就是中位數，而以用 mp.median()取得。

import numpy as np
np.random.seed(1)
data=np.random.randint(1,100, 3)
print(f'排序前 : {data}')
print(f'排序後 : {np.sort(data)}')
print(f'中位數 : {np.median(data)}')
結果 : 
排序前 : [38 13 73]
排序後 : [13 38 73]
中位數 : 38.0

偶數中位數

一組數字的數量如果是偶數，比如有 4 個數字，將這 4 個數字由小而大排序，取最中間的二個數，加總後除以2，就是中位數

import numpy as np
np.random.seed(1)
data=np.random.randint(1,100, 4)
print(f'排序前 : {data}')
print(f'排序後 : {np.sort(data)}')
print(f'中位數 : {np.median(data)}')
結果:
排序前 : [38 13 73 10]
排序後 : [10 13 38 73]
中位數 : 25.5

平均數(mean)

將所有的數相加，再除以總數，就是平均數，平均數的代號為 mean (請努力背起來)

import numpy as np
np.random.seed(1)
data=np.random.randint(1,100, 4)
print(data)
print(f'np平均數 : {np.mean(data)}')
sum=0
for i in data:
    sum+=i
print(f'手動算平均數 : {sum/len(data)}')
結果:
[38 13 73 10]
np平均數 : 33.5
手動算平均數 : 33.5

標準差(Standard deviation)

deviation[divɪˋeʃən] 越軌，偏離航道的意思

將所有的數字與平均數相減，然後平方，將其結果相加，再除以數字數量，最後再開根號。
說真的，用上述中文的說法，其實很難描述，所以請仔細並且背熟底下的公式

$(\sqrt{\frac{1}{n}\sum (x_{i}-mean)^{2}})$

標準差用於測量一組數值的離散程度，標準差愈小，則這組數值愈接近。

import numpy as np
np.random.seed(1)
data=np.random.randint(1,100, 4)
print(data)
print(f'np 標準差 : {data.std()}')
m=data.mean()

sum=0
for i in data:
    sum+=(i-m)**2
std=(sum/len(data))**0.5
print(f'手動標準差 : {std}')
結果 : 
[38 13 73 10]
np 標準差 : 25.26361019331956
手動標準差 : 25.26361019331956

$(\sum_{i=1}^{n}(x_{i}-\upsilon )^{2}=\sum_{i=1}^{N}(x_{i}^{2}-2x_{i}\upsilon +\upsilon^{2}))$
=$((\sum_{i=1}^{n}x_{i}^{2})-(2\upsilon \sum_{i=1}^{n}x_{i})+n\upsilon ^{2})$

 

開根號

將所有的數字開根號，其實就是跟大家假裝很熟的意思，跟大家的距離都拉近了

Log 10

把親人都拉進核心，但相差甚遠的人呢，盡可能的拉近，表現出大家都是一家人

當$(x=\beta^{y})$，則 $(y=\log_{\beta}x)$

$(\beta)$稱為底數

平均值與標準差

todo

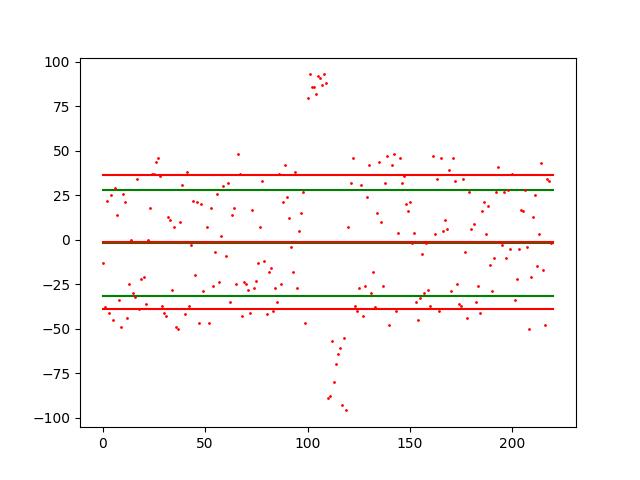
import numpy as np
import pylab as plt
np.random.seed(1)
count=100
y1=list(np.random.randint(-50,50,count))
y2=list(np.random.randint(80,100,10))
y3=list(np.random.randint(-100,-50,10))
y4=list(np.random.randint(-50,50,count))
total=len(y1)+len(y2)+len(y3)+len(y4)

yn=np.array(y1+y4)
yn_mean=yn.mean()
yn_std=yn.std()
plt.plot([0,total],[yn_mean, yn_mean],c='g')
plt.plot([0,total],[yn_mean+yn_std,yn_mean+yn_std],c='g')
plt.plot([0,total],[yn_mean-yn_std,yn_mean-yn_std],c='g')


y=np.array(y1+y2+y3+y4)
x=list(range(len(y)))
m=y.mean()
s=y.std()
s1=m+s
s2=m-s
plt.plot(x,y, 'ro', markersize=1)
plt.plot([0,total],[m,m],c='r')
plt.plot([0,total],[s1,s1],c='r')
plt.plot([0,total],[s2,s2],c='r')

plt.show()

用一個圖型來表示 todo